5 February 2021

Multivariate Data

by mervyn

source “K-MOOC 오세종 교수님의 강좌의 5. 다변량 자료의 탐색 중 (http://www.kmooc.kr/courses/course-v1:DKUK+DKUK0003+2020_T3)"

Scatter Plot

A graph that shows the distribution of bivariate data. Correlation between two variables Wide range of parameters

wt<- mtcars$wt
mpg<- mtcars$mpg
# x axis, y axis 
plot(wt, mpg, 
main="Car Weight-mpg",
xlab="car Weight",
ylab="Miles Per Gallon",
col="red",
pch=19) 

pch: type of point plot(): 2 dimensional graph, only shows the relationship between two variables pairs(): Show correlations between multiple variables

vars<- c("mpg", "disp", "drat", "wt")
target<- mtcars[,vars]
pairs(target, main="multi plots")

iris.2<- iris[,3:4] # data
point<- as.numeric(iris$Species) # point shape
color<- c("red", "green", "blue")
plot(iris.2,
main="Iris plot",
pch=c(point),
col=color[point])

Assignment

Use dataset cars, draw scatter plot on speed and dist (x axis: spped) Explain correlation between speed and dist.
Use dataset pressure, draw scatter plot on temperature and pressure. (x axis: temperature) Explain correlation between two variables.
Use dataset state.x77, draw scatter plot on population, income, illiteracy, area. Observe correlation. (use pairs() function)
In dataset iris, distribution of Sepal.Length, Sepal.Width by Species.

# 1
speed<- cars$speed
dist<- cars$dist
plot(speed, dist,
     main="Car Speed-dist",
     xlab= "Car Speed",
     ylab= "Car dist",
     col="red")
# As speed increases, dist also increases

# 2
temperature<- pressure$temperature
pressure<- pressure$pressure
plot(temperature, pressure,
     main="Pressure-Temperature",
     xlab="Temperature",
     ylab="Pressure",
     col="blue")
# As temperature increases, pressure increases exponentially.

# 3
vars<- c("Population", "Income", "Illiteracy", "Area")
target<- state.x77[,vars]
pairs(target, main= "multi plots")

# 4
head(iris)
iris.2<- iris[,1:2]
Species<- iris$Species
point<- as.numeric(Species)
color<-c("red", "green", "blue")
plot(iris.2,
     main="Length & Width by Species",
     pch= c(point),
     col= color[point])

Correlation Analysis

Two variables, two quantitative data analysis. Always used with scatter plots. Numerical representation of two variables.

Correlation Coefficient r

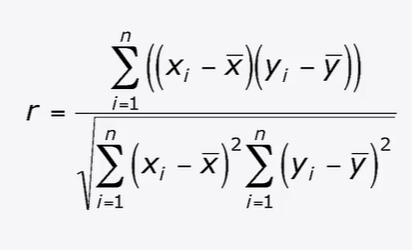
coeff

Properties of r

Distributed \(-1\leq r\leq 1\)
\(r>0\): positive correlation
\(r<0\); negative correlation
\(\lvert r\rvert\): closer to 1, higher (stronger) correlation. Closer to 0, lower (weaker) correlation.

Straighter the line is, the closer \(\lvert r\rvert\) to 1

beers=c(5,2,9,8,3,7,3,5,3,5)
bal=c(0.1, 0.03, 0.19, 0.12, 0.04, 0.095, 0.07, 0.06, 0.02, 0.05)
tbl=data.frame(cbind(beers, bal))
tbl; class(tbl)
plot(bar~beers, data=tbl) # scattered plot. plot(x, y)=plot(y~x)
res=lm(bal~beers, data=tbl) # regression equation. used to draw a line to find out what linear correlation between x and y 
# lm(): identify the line(regression equation)
abline(res) # abline(): draw a regression line
cor(beers,bal) # cor(): correlation analysis. calculate correlation coefficient

point at the bottom: the person with a low blood alcohol level point at the top: the person with the highest blood alcohol level.

The faster you can digest alcohol, the lower your blood alcohol level will be

If \(\lvert r\rvert\) > 0.5, we think there is a correlation.

data.frame: makes data into data frame cbind(): combine two vectors in column direction rbind(): combine two vectors in row direction plot(): plot(tbl), plot(tbl[,1], tbl[,2]) return same result.

Find Correlation Coefficients of multiple variables simultaneously

cor(iris[,1:4]) # analyze correlation between 4 variables

Assignment

Income	Years of Education
125,000	19
100,000	20
40,000	16
35,000	16
41,000	18
29,000	12
35,000	14
24,000	12
50,000	16
60,000	17

Analyze correlation between income and years of eduation (Scattered Plot, Correlation coefficient)

CSV file

GPA	TV in hours per week
3.1	14
2.4	10
2.0	20
3.8	7
2.2	25
3.4	9
2.9	15
3.2	13
2.7	4
2.5	21

Analyze correlation between grade and TV watch. (Scattered Plot, Correlation Coefficient)

[CSV file](/assets/Lc5_2_2.csv

# 1
mydata<- read.csv(file.choose(), header=TRUE)
is.vector(mydata)
is.data.frame(mydata)
mydata; class(mydata) # show mydata
plot(mydata)
corr1<- plot(mydata)

# 2
mydata<- read.csv(file.choose(), header=TRUE)
is.vector(mydata)
is.data.frame(mydata)
plot(mydata)
corr2<- plot(mydata)

Line Graph

Used when one of the variables is time: Time Series Analysis.

month=1:12
late=c(5, 8, 7, 9, 4, 6, 12, 13, 8, 6, 6, 4)
plot(month, # x data # time data
     late, # y data # late students data
     main="Late students", # title of graph
     type="l", # type of graph (in alphabet)
     lty=1, # Line type
     lwd=1, # boldness of line
     xlab="Month", # x axis label
     ylab="Late cnt") # y axis label

type=”l”: line type=”b”: dotted line type=”s”: ladder line type=”o”: overlapped dots and line type=”h”: vertical line for value type=”S”: ladder line 2

Line type

No.1: ‘solid’ No.2: ‘dashed’ No.3: ‘dotted’
No.4: ‘dotdash’ No.5: ‘longdash’ No.6: ‘twodash’

Drawing Multiple Line Graphs

overlapping line graphs

plot(month, # first graph # x data
     late1,		  # y data
     main="Late students",
     type="b",		  # type of graph
     lty=1,		  # line type
     col="red",		  # color of line
     xlab="Month",
     ylab="Late cnt")

lines(month,    # overlapping graph
      late2,
      type="b",
      col="blue")

If there are multiple variables, we can represent as a graph by keep adding line function.

Assignment

Draw a line graph
Draw a line graph

Year= 2015:2026
Total.Population=c(51014, 51245, 51446, 
                   51635, 51811, 51973, 
                   32123, 52261, 52338, 
                   52504, 52609, 52704)
plot(Year,
     Total.Population,
     main="Predicted Population",
     type="l",
     lty=1,
     lwd=1,
     xlab="Year",
     ylab="Population")


Year=c(20144, 20151:20154, 
      20161:20164, 20171:20173)
Male=c(73.9, 73.1, 74.4, 
       74.2, 73.5, 73.0, 
       74.2, 74.5, 73.8, 
       73.1, 74.5, 74.2)
Female=c(51.4, 50.5, 52.4,
         52.4, 51.9, 50.9, 
         52.6, 52.7, 52.2, 
         51.5, 53.2, 53.1)
plot(Year, Male,
     main="Economic Activity",
     type="b",
     # lty=1,
     col="red",
     xlab="Year",
     ylab="Participation")
lines(Year, Female,
      type="b",
      col="blue")

Data Analysis Example: iris

Dataset general information

str(iris) # all information
class(iris) # data structure
head(iris) # front matters of the data
dim(iris) # number of row and column
table(iris$Species) # how many measurements of species and how many samples

Data distribution for each column

summary(iris[,1]) # min, max, median, mean values
summary(iris[,2])
summary(iris[,"Petal.Length"])
summary(iris$Petal.Width)
sd(iris[,1]) # Sepal.Length
sd(iris[,2]) # Sepal.Width
sd(iris[,3]) # Petal.Length
sd(iris[,4]) # Petal.Width

min/max

range of data
distribution range

mean/median

average value of data
if mean & median is similar(identical): complete normal distrition
if wide gap between two: leans toward something

sd(): range of distribution

small: variables are clustered together on the average
big: widely distributed on the average

Data distribution of each column by group Use boxplot

par(mfrow=c(2,2))
boxplot(Sepal.Length~Species, data=iris,
        main="Sepal.Length")
boxplot(Sepal.Width~Species, data=iris,
	main="Sepal.Width")
boxplot(Petal.Length~Species, data=iris,
	main= "Petal.Length")
boxplot(Petal.Width~Species, data=iris,
	main="Petal.Width")

Data distritbution of each column by group Using scatter plot

point<- as.numeric(iris$Species)
color<-c("red", "green", "blue")
pairs(iris[,-5],
      pch=c(point),
      col=color[iris[,5]]
)

if two colors are mixed, we can not distinguish two species with that data. if the color is separated from others, the species is different with others.

cor(): positive, negative, strong, weak correlation

Assignment

Analysis dataset state.x77 Add state.region to state.x77

Hint:

st<- data.frame(state.x77, state.region)
head(st)

st<- data.frame(state.x77, state.region)
head(st)

# Step 1
str(st)
class(st)
table(st$state.region)

# Step 2
summary(st[,1]) # Population
summary(st[,2]) # Income
summary(st[,"Illiteracy"])
summary(st$Life.Exp)
sd(st[,5]) # Murder
sd(st[,"HS.Grad"])

# Step 3
par(mfrow=c(2,2))
boxplot(Frost~state.region,
        data=st,
        main="Frost by State")
boxplot(Population~Area, 
        data=st,
        main="Population by Area")

# Step 4
point<- as.numeric(st$state.region)
Murder<- st$Murder
Income<- st$Income
Illiteracy<- st$Illiteracy
Life.Exp<- st$Life.Exp
HS.Grad<- st$HS.Grad
color<- c("red", "green", "blue", "yellow", "grey")
pairs(Murder~Income+Illiteracy+Life.Exp+HS.Grad,
      pch=c(point),
      col=color[point])

back next Index

tags: R

Comments

Post comment

Data Journey

International Studies Grad. racing for AI Engineer

Multivariate Data

Scatter Plot

Assignment

Correlation Analysis

Find Correlation Coefficients of multiple variables simultaneously

Assignment

Line Graph

Drawing Multiple Line Graphs

Assignment

Data Analysis Example: iris

Assignment

Comments

Multivariate Data

Scatter Plot

Assignment

Correlation Analysis

Find Correlation Coefficients of multiple variables simultaneously

Assignment

Line Graph

Drawing Multiple Line Graphs

Assignment

Data Analysis Example: iris

Assignment

Comments

Share this: