Binary Heaps: Implementation

Perfect Binary Trees

A perfect binary tree of height h is a binary tree where

• All leaf nodes have the same depth h
• All other nodes are full
• Have only two children Recursive definition:
• A binary tree of height h =0 is perfect
• A binary tree with height h > 0 is a perfect if both sub-trees are perfect binary trees of height h-1
• Perfect binary trees of height h = 0, 1, 2, 3, and 4

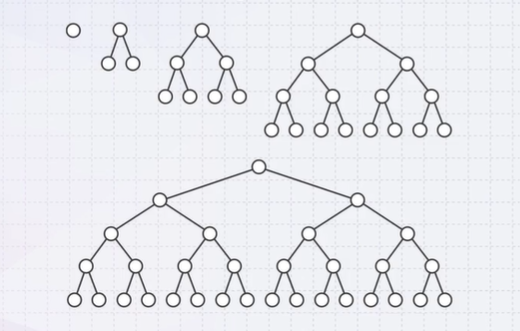
• A perfect binary tree has ideal properties but restricted in the number of nodes : \(n = 2^h -1\)

Complete Binary Trees

We require binary trees which are

• Similar to perfect binary trees, but
• Defined for all n A complete binary tree filled at each depth from left to right
• The order is identical to that of a breadth-first traversal
• The height of a complete binary tree with n nodes is \(h = [\lg n]\) The previous heap may be represented as the following (non-unique) complete tree:

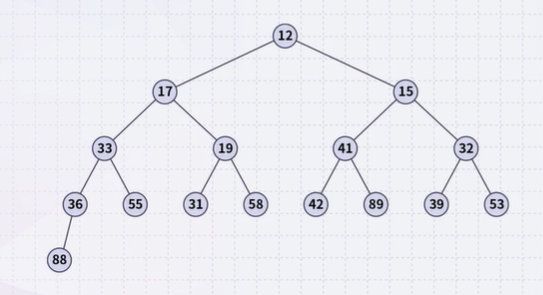
• Push: If we insert into a complete tree, we only need to place the new node as a leaf node in the appropriate location and percolate up -> resulting tree is still a complete tree

• Pop:

  Percolating up creates a hole leading to a non-complete tree

  -> Alternatively, copy the last entry in the heap to the root

  -> percolate the original node down swapping it with the smallest of its children

  -> halt when both children are larger

  -> the resulting tree is still a complete tree

  -> in the last pop, the last entry percolated down to the point where it has no children

  Therefore, we can maintain the complete-tree shape of a heap using BFS order

We may store a complete tree using an array:

• A complete tree is filled in breadth-first traversal order
• The array is filled using breadth-first traversal

Array Implementation

A breadth-first traversal yields: If we associate an index-starting at 1-with each entry in the breadth-first traversal, we get:

Given the entry at index k, it follows that:

• The parent of node is a k/2
• The children are at 2k and 2k+1 (Trivial) Cost: start array at position 1 instead of position 0
• If the heap-as-array has count entries, then the next empty node in the corresponding complete tree is at location posn=count+1
• We compare the item at location posn with the item at posn/2
• If they are out of order
  • Swap them, set posn/=2 and repeat

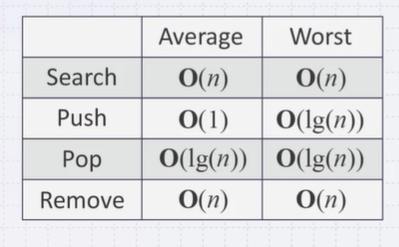
Runtime Analysis

• Accessing the top object is \(\Theta(1)\)
• Popping the top object is \(O(lg(n))\)
  • We copy something that is already in the lowest depth
    • it will likely be moved back to the lowest depth
• Push:
• If we are inserting an object less than the root (at the front), then the run time will be \(\Theta(lg(n))\)
• If we insert at the back (greater than any object) then the run time will be \(\Theta(1)\)
• Arbitrary insertion
  • With each percolation, it will move an object past half of the remaining entries in the tree
    • Therefore after one percolation, it will probably be past half of the entries, and therefore on average will require no more percolations
    \[\frac{1}{n}\sum_{k=0}^{h}(h-k)2^k= \frac{2^{k+1}-h-2}{n}= \frac{n-h-1}{n}=\Theta(1)\]
    • Therefore, we have an average run time of \(\Theta(1)\)
  • An arbitrary removal requires that all entries in the heap be checked: \(O(n)\)
  • A removal of the largest object in the heap still requires all leaf nodes to be checked - there are approximately n/2 leaf nodes: \(O(n)\)

  

Binary Max Heaps

A binary max-heap is identical to a binary min-heap except that the parent is always larger than either of the children

• The only difference: the root node has the maximum value in case of the min heap
• Same algorithm can be applied Example: same data as before stored as a max-heap yields

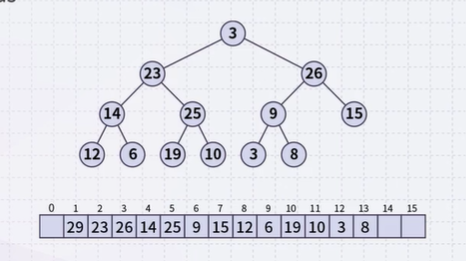
source “K-MOOC 허재필 교수님의 <인공지능을 위한 알고리즘과 자료구조: 이론, 코딩, 그리고 컴퓨팅 사고> 강좌의 9-2 힙 자료구조의 구현 및 복잡도 중(http://www.kmooc.kr/courses/course-v1:SKKUk+SKKU_46+2020_T1)”

back next

Comments

Post comment

Loading...