Binary Heaps

Definition

A non-empty binary tree is an min-heap if

• The key associated with the root is less than or equal to the keys associated with either of the sub-trees (if any)
• Both sub-trees (if any) are also binary min-heaps

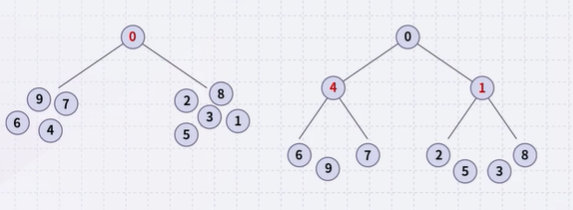
• A single node is a min-heap
• All keys in either sub-tree are greater than the root key Important
  • There is no other relationship between the elements in the two subtrees

Example

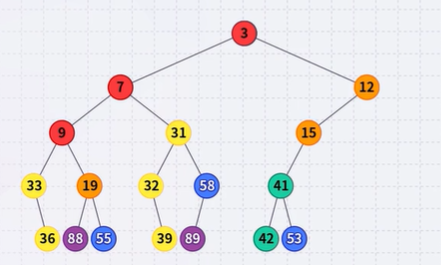
• The left subtree has the smallest (7) and the largest (89) objects
• No relationship between items with similar priority

Operations

Three operations:

• Top: we can find the top object in \(\Theta(1)\) time
• Pop: to remove the minimum object
  • remove the root node
  • promote the node of the sub-tree which has the least value
  • Recurs down the sub-tree from which we promoted the least value
• Push: inserting into a heap may be done either
  • At a leaf (move it up if it is smaller than the parent)

    • binary min-heap use the one

      Select an arbitrary node to insert a new leaf node

      If both the left and right subtrees of the node were greater than the node, we are guaranteed that we don’t have to send the new node down.

      This process is called percolation, that is, the lighter (smaller) objects move up from the bottom of the min-heap

  • At the root (insert the larger object into one of the subtrees)
    • Other heaps use the second

source “K-MOOC 허재필 교수님의 <인공지능을 위한 알고리즘과 자료구조: 이론, 코딩, 그리고 컴퓨팅 사고> 강좌의 9-1 힙 자료구조의 정의와 연산 중(http://www.kmooc.kr/courses/course-v1:SKKUk+SKKU_46+2020_T1)”

back next

Comments

Post comment

Loading...