Merge Sort

Merge Sort

The merge sort algorithm is defined recursively:

• If the list is of size 1, it is sorted-we are done;
• Otherwise:
• Divide an unsorted list into two sub-lists,
• Sort each sub-list recursively using merge sort, and
• Merge the two sorted sub-lists into a single sorted list This is the first significant divide-and-conquer algorithm we will see.
• Question: How quickly can we recombine the two sub-lists into a single sorted list?

Merging Example

Merge sort contains three things:

• 2 sub-array already sorted,
• 1 combined, merged array that has the output of the 2 sub-array.
  1. Consider the two sorted arrays and an empty array.

3, 5, 18, 21, 24, …

2, 7, 12, 16, 33, …

1. Define three indices at the start of each array.
2. Compare 2 and 3: 2 < 3
   • Copy 2 down
   • Increment the corresponding indices

Compare 3 and 7: 3 < 7

• Copy 3 down
• Increment the corresponding indices

Compare 5 and 7: 5 < 7

• Copy 5 down
• Increment the corresponding indices

Compare 18 and 7: 7 < 18

• Copy 7 down
• Increment the corresponding indices

Compare 18 and 12: 12 < 18

• Copy 12 down
• Increment the corresponding indices

Compare 18 and 16: 16 < 18

• Copy 16 down
• Increment the corresponding indices

Compare 33 and 18: 18 < 33

• Copy 18 down
• Increment the corresponding indices

Compare 21 and 33: 21 < 33

• Copy 21 down
• Increment the corresponding indices

Compare 24 and 33: 24 < 33 - Copy 24 down - Increment the corresponding indices

1. Continue until we have passed beyond the limit of one of the two arrays. == One of the sub-arrays gets ended (copied every element from 3 to 31 and there’s no more elements to compare in this sub-array)

2. Copy over all remaining entries in the non-empty array (copy from 33 to 42 sequentially from the second sub-array to the result array)

Merging Two (Sorted) Arrays

Programming a merge is straight-forward:

• the sorted arrays, arrayA and arrayB, are of size nA and nB, respectively, and
• we have an empty array, arrayOut, of size nA+nB
• define three variables, posA = 0, posB = 0, k = 0; which index into these three arrays

Implementation

template <typename Type>
void Merge(Type *_arrayA, Type *_arrayB, int _nA, int _nB, Type *_arrayOut){
  int posA = 0, posB = 0, k = 0;
  while(posA < _nA && posB < _nB){
    if(_arrayA[posA]< _arrayB[posB]){
      _arrayOut[k] = _arrayA[posA];
      posA++;
    }
    else{
      _arrayOut[k] = _arrayB[posB];
      posB++;
    }
    k++;
  }
  for(; posA < _nA; posA++){
    _arrayOut[k] = _arrayA[posA];
    k++;
  }
  for(; posB< _nB; posB++){
    _arrayOut[k] = _arrayB[posB];
    k++;
  }
}

Problem of Merging

We cannot merge two arrays in-place

• This algorithm always require the allocation of a new array

Algorithm

1. Split the list into two approximately equal sub-lists
2. Recursively call merge sort on both sub lists
3. Merge the resulting sorted lists

Merge-Sort(A, p, r)

if p < r
   q = [(p + r)/2]
   Merge-Sort(A, p, q)
   Merge-Sort(A, q+1, r)
   Merge(A, p, q, r)

• Question: We split the list into two sub-lists and sort them. How should we sort these lists?
• Answer(theoretical):
• If the side of these sub-lists is >1, use merge sort again
• If the sub-lists are of length 1, do nothing; a list of length one is sorted
• Answer(practical):
• If the sub-lists are less than some threshold length, use an algorithm like insertion sort to sort the lists
• Otherwise, use merge sort, again

Implementation

Suppose that we already have a function

template <typename Type>
void Merge(Type *array, int first, int midpoint ,int last)

that assumes that the entries

array[first] through array[midpoint - 1], and
array[midpoint] through array[last - 1]

are sorted and merges these two sub-arrays into a single sorted array from index ‘first’ though index ‘last-1’. We will therefore implement a function

template <typename Type>
void Merge_Sort(Type *array, int first, int last)

that will sort the entries in the positions \(first \leq i < last\) If the number of entries is less than \(n_{T}\), call insertion sort Otherwise:

1. Find the mid-point
2. Call merge sort recursively on each of the halves, and
3. Merge the results

template <typename Type>
void Merge_Sort(Type *array, int first, int last){
  if(_last - _first <= NUM_THRESHOLD){
    Insertion_Sort<Type>(_array, _first, _last);
  }// $$T(1)= T(2)= ... = T(N_{T})= \Theta(1)$$
  else{
    int midpoint=(_first + _last)/2;// $$\Theta(1)$$

    Merge_Sort<Type>(_array, _first, midpoint);//$$T\left ( \frac{n-1}{2} \right )$$
    Merge_Sort<Type>(_array, midpoint, _last);//$$T\left ( \frac{n-1}{2} \right )$$
    Merge(_array, _first, midpoint, _last);// $$\Theta(n)$$ linear time
  }  
}

Recursive Functions-Merge Sort

Recursion three Given a recurrence: \(T(n)\) = {if \(n = 1\), \(\Theta(1)\) {if \(n > 1\), \(2T(n/2)+\Theta(n)\) We first rewrite the recurrence as follows: \(T(n)\) = {if \(n = 1\), \(c\) {if \(n > 1\), \(2T(n/2) +cn\)

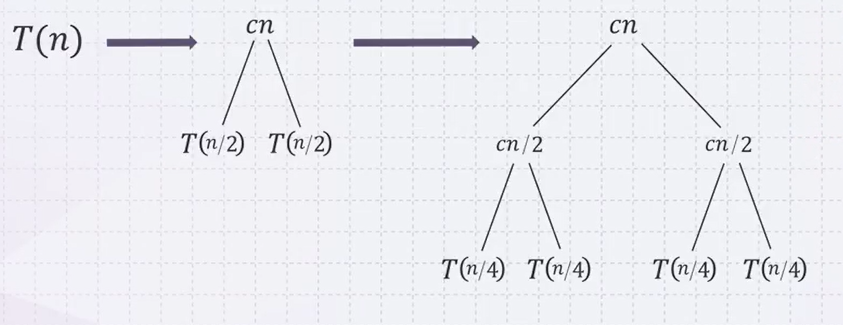
Total Time Complexity: \(\Theta(n lg n)\)

source “K-MOOC 허재필 교수님의 <인공지능을 위한 알고리즘과 자료구조: 이론, 코딩, 그리고 컴퓨팅 사고> 강좌의 7-2 합병 정렬과 재귀적 알고리즘의 복잡도 분석 중(http://www.kmooc.kr/courses/course-v1:SKKUk+SKKU_46+2020_T1)”

back next

Comments

Post comment

Loading...