Asymptotic Analysis_02

\(\Theta\) - Notation

\(\Theta\) - Notation (theta)

• A function \(f(n)=\Theta(g(n))\) if there exist positive constants \(n_{0}, n_{1}\), and \(n_{2}\) such that \(0 \leq c_{1}g(n) \leq f(n) \leq c_{2}g(n)\) for all \(n \geq n_{0}\)

• \(f(n)\) has a rate of growth equal to that of \(g(n)\)
  • \(f(n)\) belongs to \(\Theta(g(n))\)
  • \(g(n)\) is an asymptotically tight bound for \(f(n)\)
  • If \(f(n)=\Theta(g(n))\) is a polynomial of degree k, then \(f(n)=\Theta(n^k)\)

Example:

• \[\frac{1}{2}n^2 - 3n = \Theta (n^2)\]
• \(\frac{1}{14}n^2 \leq \frac{1}{2}n^2 - 3n\leq n^2\), for all \(n\geq 7\)
• \(an^2+bn+c=\Theta(n^2)\), when \(a>0\)
• \[c_{1}=\frac{a}{4}, c_{2}=\frac{7a}{4}, n_{0}=2 max(\frac{|b|}{a}, \sqrt{\frac{|c|}{a}})\]

O - Notation

O - Notation (big-oh)

• A function \(f(n)=\Theta(g(n))\) if there exist positive constants \(c\) and \(n_{0}\) such that \(0\leq f(n)\leq cg(n)\) for all \(n \geq n_{0}\)
• Any algorithm that is an O(n) is also \(O(n log n), O(n^2), O(n^3), O(2^n)\) and also anything else that’s asymptotically bigger than n.

• \(g(n)\) is an asymptotically upper bound for \(f(n)\)
• \(f(n)=\Theta(g(n))\) implies \(f(n)=O(g(n))\)
• O is suitable to bound the worst-case running time.

Example:

• \[2n^2+8n-2=O(n^2)\]
• \[2n^2+8n-2=O(n^3)\]
• \[2n^2+8n-2=O(n^4)\]
• \[2n^2+8n-2\neq O(n)\]

\(\Omega\) - Notation

\(\Omega\) - Notation (omega)

• A function \(f(n)=\Omega(g(n))\) if there exist positive constants \(c\) and \(n_{0}\) such that \(0 \leq cg(n) \leq f(n)\) for all \(n \geq n_{0}\)

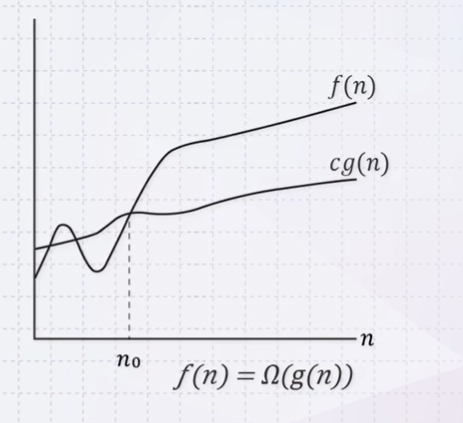
• \(g(n)\) is an asymptotically lower bound for \(f(n)\)
• \(f(n)=\Theta(g(n))\) implies \(f(n)=\Omega(g(n))\)
• \(\Omega\) is suitable to bound the best-case running time.
• \(f(n)=\Theta(g(n))\) if and only if \(f(n)=O(g(n))\) and \(f(n)=\Omega(g(n))\)

Asymptotic Notation in Equations (or Inequalities)

• In general, asymptotic notations appeared in equations are interpreted as some anonymous function Examples:
  • \[2n^2+3n+1 = 2n^2+\Theta(n)\]
  • \[T(n)=2T(\frac{n}{2})+\Theta(n)\]

o - Notation

O - notation (big-oh) may or may not be asymptotically tight

• \(2n^2 =O(n^2)\rightarrow\) asymptotically tight, \(2n= O(n^2)\rightarrow\) not tight o - notation (little-oh)
• A function \(f(n)=o(g(n))\) if there exist a positive constant \(n_{2}\) such that \(0 \leq f(n) < cg(n)\) for all \(n \geq n_{0}\) and all constant \(c>0\)
  • \(g(n)\) is an upper bound of \(f(n)\) that is not asymptotically tight

Examples: - \(2n=o(n^2)\) but \(2n^2\neq o(n^2)\)

\(\omega\) - Notation

\(\omega\) - notation (little-omega)

• A function \(f(n)=\omega(g(n))\) if there exist a positive constant \(n_{0}\) such that \(0 \leq cg(n) < f(n)\) for all \(n > n_{0}\) and all constant \(c>0\)
  • \(g(n)\) is an lower bound of \(f(n)\) that is not asymptotically tight Examples:
  • \(2n^2=\omega(n)\) but \(2n^2\neq \omega(n^2)\)
• Theta notation and Big-O notation are used most often.

Properties of Notations

• Transivity
  • \(f(n)=\Theta(g(n))\) and \(g(n)=\Theta(h(n))\) imply \(f(n)=\Theta(h(n))\)
  • It is true for o, O, \(\omega\), and \(\Omega\)
• Reflexivity
  • \[f(n)=\Theta(f(n))\]
  • It is true for O and \(\Omega\)
• Symmetry
  • \(f(n)=\Theta(g(n))\) if and only if \(g(n)=\Theta(f(n))\)
• Transpose symmetry
  • \(f(n)=O(g(n))\) if and only if \(g(n)=\Omega(f(n))\)
  • \(f(n)=o(g(n))\) if and only if \(g(n)=\omega(f(n))\)

Notations Defined with Limit

notations	limit
\(f(n)=o(g(n))\)	\(\lim_{n\rightarrow \infty}\frac{f(n)}{g(n)} =0\)
\(f(n)=O(g(n))\)	\(\lim_{n\rightarrow \infty}\frac{f(n)}{g(n)} < \infty\)
\(f(n)=\Theta(g(n))\)	\(0<\lim_{n\rightarrow \infty}\frac{f(n)}{g(n)} < \infty\)
\(f(n)=\Omega(g(n))\)	\(\lim_{n\rightarrow \infty}\frac{f(n)}{g(n)} > 0\)
\(f(n)=\omega(g(n))\)	\(\lim_{n\rightarrow \infty}\frac{f(n)}{g(n)} = \infty\)

Common Classes

• The most common classes are given names:

  classes	names
  \(\Theta(1)\)	constant
  \(\Theta(lg(n))\)	logarithmic
  \(\Theta(n)\)	linear
  \(\Theta(n lg(n))\)	“n log n”
  \(\Theta(n^2)\)	quadratic
  \(\Theta(n^3)\)	cubic
  \(2^n, e^n, 4^n, ...\)	exponential

Weak Ordering

Algorithm Analysis

We will use the notations to describe the complexity of algorithms

• e.g.: Adding a list of n floats will be said to be a \(\Theta(n)\) algorithm.
• An algorithm is said to have polynomial time complexity if its runtime is described by \(O(n^d)\) for some fixed \(d\geq 0\)
  • We will consider such algorithms to be efficient
• Problems that have no known polynomial-time algorithms are said to be intractable
  • e.g.: Travelling salesman problem (TSP)
    • Best run-time: \(\Theta(n^{2}2^{n})\)

source “K-MOOC 허재필 교수님의 <인공지능을 위한 알고리즘과 자료구조: 이론, 코딩, 그리고 컴퓨팅 사고> 강좌의 5-2 심볼 기반 함수의 점근적 바운드 중(http://www.kmooc.kr/courses/course-v1:SKKUk+SKKU_46+2020_T1)”

back next

Comments

Post comment

Loading...