Non-Linear Data Structure: Graph

Graph

A graph is a data type for storing adjacency relations.

• Objects: a finite set of nodes (or vertices)
• Relationships: a finite set of edges (or arcs, links) Examples: Computer networks, Road networks, Circuits, CS curriculum

Undirected Graphs

We define an undirected graph as a collection of vertices \(V = \{v_{1}, v_{2}, ..., v_{n}\}\)

• The number of vertices is denoted by \(\lvert V \rvert\) = n
• Associated with this is a collection E of unordered pairs \({ v_{i}, v_{j}}\) termed edges which connect the vertices There are a number of data structures that can be used to implement graphs
• Adjacency matrices
• Adjacency lists
• We will assume in this course that a vertex is never adjacent to itself
  • For example, \({ v_{1}, v_{2}}\) will not define an edge The maximum number of edges in an undirected graph is

\[| E |\leq \binom{| V |}{2}= \frac{| V | ( | V |-1 )}{2}=O ( | V |^{2} )\]

Example 01

Consider this collection of vertices \(V = {v_{1}, v_{2}, ..., v_{9}}\) where \(\lvert V\rvert\) = 9

Associated with these vertices are \(\lvert E \rvert\)=5 edges

\[E = \{ \{ v_{1}, v_{2}\},\{ v_{3}, v_{5}\},\{ v_{4}, v_{8}\},\{ v_{4}, v_{9}\},\{ v_{6}, v_{9}\}\}\]

• The pair \({ v_{j}, v_{k}}\) indicates that both vertex \(v_{j}\) is adjacent to vertex \(v_{k}\) and vertex \(v_{k}\) is adjacent to vertex \(v_{j}\)

Example 02

Given the \(\lvert V\rvert\)=n vertices A, B, C, D, E, F, G and the \(\lvert E\rvert\)=9 edges

Degree

The degree of a vertex is defined as the number of adjacent vertices

degree(A) = degree(D) = degree(C) = 3

degree(B) = degree(E) = 4

degree(F) = 1 degree(G) = 0

• Those vertices adjacent to a given vertex are its neighbors

Sub-Graphs

A sub-graph of a graph: a subset of the vertices and a subset of the edges that connected the subset of vertices in the original graph

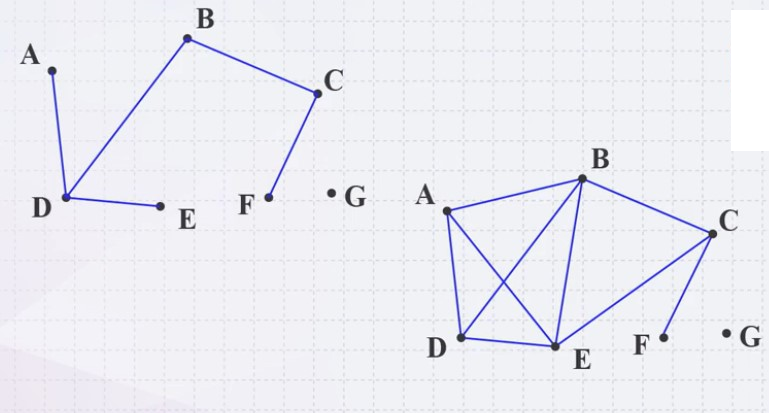
Paths

A path in an undirected graph is an ordered sequence of vertices \(( v_{1}, v_{2}, ..., v_{k})\)

Where \({ v_{j-1}, v_{j}}\) is an edge for j = 1, …, k

• Termed a path from \(v_{0}\) to \(v_{k}\)
• The length of this path is k

Example

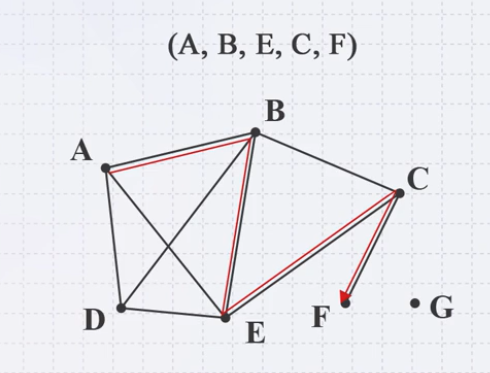
• A path of length 4

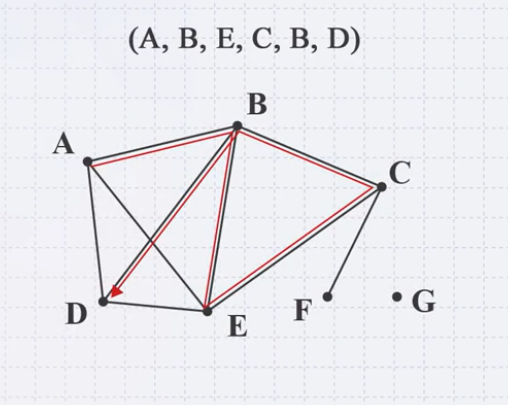
• A path of length 5

• A trivial path of length 0

Simple Paths

• A simple path has no repetitions other than perhaps the first and last vertices (e.g.: A-B-C-A)
• A simple cycle is a simple path of at least two vertices with the first and last vertices equal
• What is the example of “simple cycle”?

Connectedness

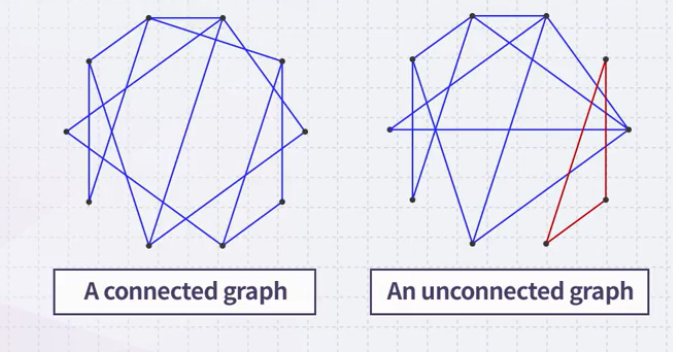
• Two vertices \(v_{i}, v_{j}\) are said to be connected if there exists a path from \(v_{i}\) to \(v_{j}\)
• A graph is connected if there exists a path between any two vertices

Weighted Graphs

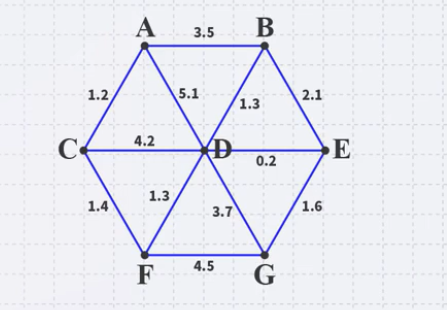
• A weight may be associated with each edge in a graph
• This could represent distance, energy consumption, cost, etc.
• Such a graph is called a weighted graph
• Pictorially, we will represent weights by numbers next to the edges
• The length of a path within a weighted graph is the sum of all of the edges which make up the path
  • The length of the path (A, D, G) in the above graph is 5.1 + 3.7 = 8.8
• Different paths may have different weights
  • Another path is (A, C, F, G) with length 1.2 + 1.4 + 4.5 = 7.1 Problem: find the shortest path between two vertices
  • Here, the shortest path from A to H is (A, C, F, D, E, G) with length 5.7

Trees

A graph is a tree if it is connected and there is a unique path between any two vertices

• Three trees on the same eight vertices

• Consequences:
  • The number of edges is \(\lvert E \rvert = \lvert V \rvert -1\) (\(\lvert V \rvert\): number of nodes)
  • The graph is acyclic, that is, it does not contain any cycles
  • Adding one more edge must create a cycle
  • Removing any one edge creates two disjoint non-empty sub-graphs

Forests

A forest is any graph that has no cycles

• The collection of the tree. A forest removes the connectedness constraint from the tree.
• Consequences:
  • The number of edges is \(\lvert E \rvert < \lvert V \rvert\)
  • The number of trees is \(\lvert V \rvert - \lvert E \rvert\)
  • Removing any one edge adds one more tree to the forest

Here is a forest with 22 vertices and 18 edges

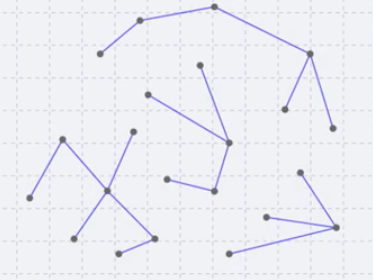
• There are four trees

Directed Graphs

In a directed graph, the edges on a graph are be associated with a direction

• Edges are ordered pairs \((v_{j}, v_{k})\) denoting a connection from \(v_{j}\) to \(v_{k}\)
• The edge \((v_{j}, v_{k})\) is different from the edge \((v_{k}, v_{j})\)

Example

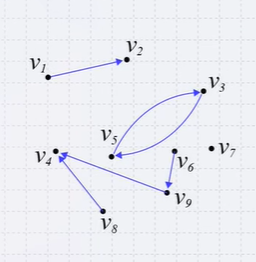
• Given our graph of nine vertices \(V = { v_{1}, v_{2}, ..., v_{9}}\)
  • These six pairs \((v_{k}, v_{j})\) are directed edges

\[E = \{ \{ v_{1}, v_{2}\},\{ v_{3}, v_{5}\},\{ v_{5}, v_{3}\}, \{ v_{6}, v_{9}\},\{ v_{8}, v_{4}\},\{ v_{9}, v_{4}\}\}\]

In and Out Degrees

The degree of a vertex must be modified to consider both cases:

• The out-degree of a vertex is the number of vertices which are adjacent to the given vertex
• The in-degree of a vertex is the number of vertices which this vertex is adjacent to
• In this graph:

in_degree(\(v_{1}\)) = 0	out_degree(\(v_{1}\)) = 1
in_degree(\(v_{5}\)) = 1	out_degree(\(v_{5}\)) = 1

Sources and Sinks

Sources and Sinks

• Vertices with an in-degree of zero are described as sources
• Vertices with an out-degree of zero are described as sinks
• In this graph:
  • Sources: \(v_{1}\), \(v_{6}\), \(v_{7}\), \(v_{8}\)
  • Sinks: \(v_{2}\), \(v_{4}\), \(v_{7}\)

Paths

• A path in a directed graph is an ordered sequence or vertices \(( v_{1}, v_{2}, ..., v_{k})\) where \({ v_{j-1}, v_{j}}\) is an edge for j = 1, …, k
• A path of length 5 in this graph is \(( v_{1}, v_{4}, v_{5}, v_{3}, v_{5}, v_{2})\)
• A simple cycle of length 3 is \(( v_{8}, v_{4}, v_{5}, v_{8})\)

Connectedness

Two vertices \(v_{j}\), \(v_{k}\) are said to be connected if there exists a path from \(v_{j}\) to \(v_{k}\)

• A graph is strongly connected if there exists a directed path between any two vertices
• A graph is weakly connected if there exists a path between any two vertices that ignores the direction
• In this graph:
  • The sub-graph \(\{ v_{3}, v_{4}, v_{5}, v_{8}\}\) is strongly connected
  • The sub-graph \(\{ v_{1}, v_{2}, v_{3}, v_{4}, v_{5}, v_{8}\}\) is weakly connected

Weighted Directed Graphs

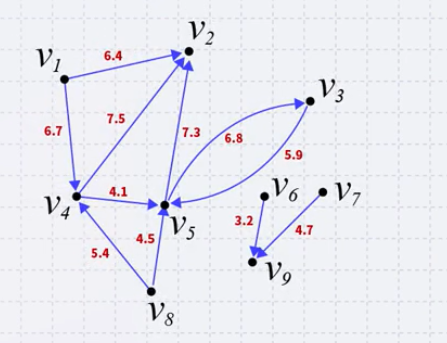
In a weighted directed graphs, each edges is associated with a value

• Unlike weighted undirected graphs, if both \(( v_{j}, v_{k})\) and \(( v_{k}, v_{j})\) are edges, it is not required that they have the same weight

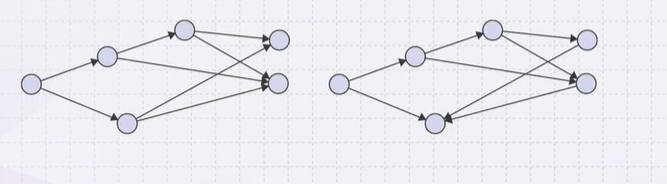
Directed Acyclic Graphs (DAG)

A directed acyclic graph is a directed graph which has no cycles

• These are commonly referred to as DAGs
• They are graphical representations of partial orders on a finite number of elements
• These two are DAGs:

Representations

How do we store the adjacency relations?

• Binary-relation list
• Adjacency matrix
• Adjacency list

Binary-Relation List

• The most inefficient is a relation list:
  • A container storing the edges
  • Requires \(\Theta(\lvert E \rvert)\) memory
  • Determining if \(v_{j}\) is adjacent to \(v_{k}\) is \(\Theta(\lvert E \rvert)\)
  • Finding all neighbors of \(v_{j}\) is \(\Theta(\lvert E \rvert)\)

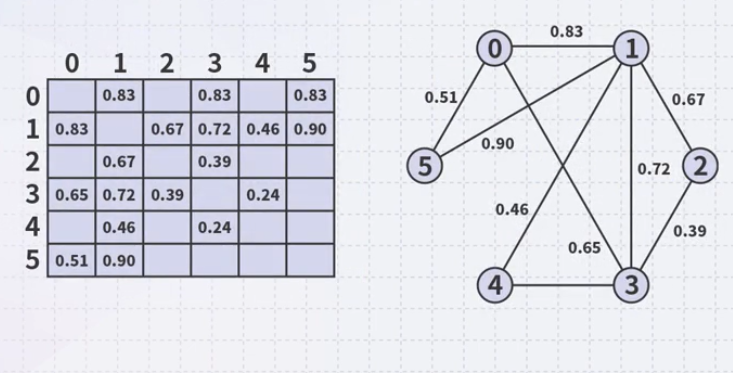
Adjacency Matrix

• Requiring more memory but also faster, an adjacency matrix
  • The matrix entry (j, k) is set to true if there is an edge \(( v_{j}, v_{k})\)
  • Requires \(\Theta(\lvert V \rvert^{2})\) memory
  • Determining if \(v_{j}\) is adjacent to \(v_{k}\) is \(\Theta(1)\)
  • Finding all neighbors of \(v_{j}\) is \(\Theta(\lvert V \rvert)\)
  • Most efficient for existence of an edge between \(v_{j}\) and \(v_{k}\)
• Adjacency matrix of a weighted graph:
  • Put the weight value to the cell

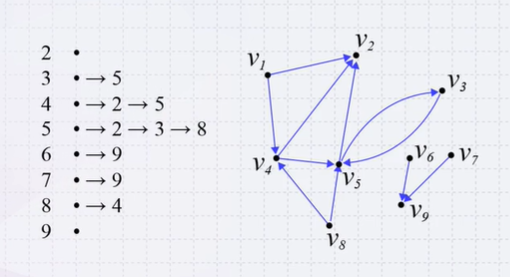
Adjacency List

• Most efficient for algorithms is an adjacency list
  • Each vertex is associated with a list of its neighbors
  • Requires \(\Theta(\lvert V\rvert + \lvert E \rvert)\) memory

source “K-MOOC 허재필 교수님의 <인공지능을 위한 알고리즘과 자료구조: 이론, 코딩, 그리고 컴퓨팅 사고> 강좌의 3-2 강좌의 그래프 자료구조 중(http://www.kmooc.kr/courses/course-v1:SKKUk+SKKU_46+2020_T1)”

back next

Comments

Post comment

Loading...