Non-Linear Data Structure: Tree
by mervyn
Tree
A collection of nodes to represent a hierarchical relationship
- Information is stored in nodes
- There is a first node, or root
- Each node has variable number of successors (children)
- Each node (other than the root) has exactly one node (parent) pointing to it. Example: Directory structures
Trees
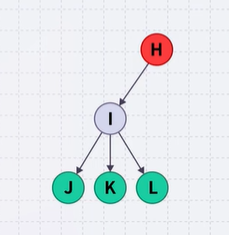
All nodes will have zero or more child nodes or children
- I has three children: J, K, and L All nodes other than the root node, there is one parent node.
- H is the parent of I The degree of a node is defined as the number of its children:
- deg(I) = 3 Nodes with the same parent are siblings
- J, K, and L are siblings
Leaf and Internal Nodes
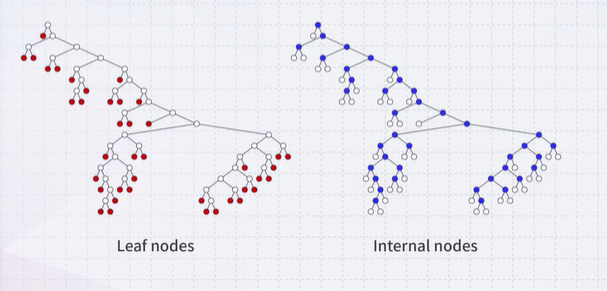
- Nodes with degree zero (zero children) are also called leaf nodes.
- All other nodes are said to be internal nodes.
Unordered & Ordered
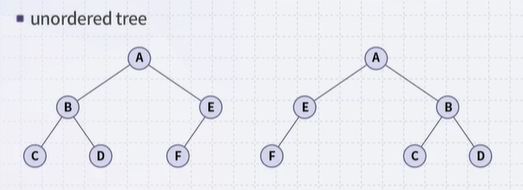
- These trees are equal if the order of the children is ignored: unordered tree
- They are different if order is relevant: ordered trees
Paths
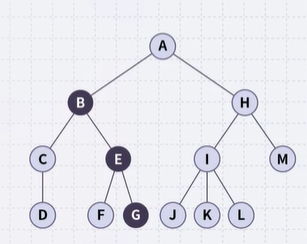
A path is a sequence of nodes (\(a_{0}\), \(a_{2}\), … , \(a_{n}\)), where \(a_{k+1}\) is a child of \(a_{k}\).
- The length of this path is n
- The path (B, E, G) has length 2
Depth
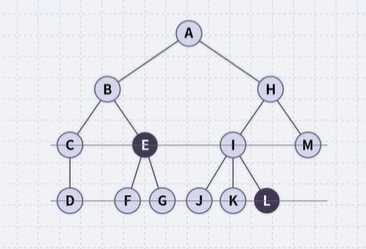
For each node in a tree, there exists a unique path from the root node to that node.
- The length of this path is depth of the node.
- E has depth 2
- L has depth 3
Height

The height of a tree is defined as the maximum depth of any node within the tree
- The height of a tree within one node is 0
- Just the root node
- For convenience, we define the height of the empty tree to be -1
Ancestor and Descendant
- If a path exists from node a to node b
- a is an ancestor of b
- b is a descendent of a Thus, a node is both an ancestor and a descendent of itself
- We can add the adjective strict to exclude equality: a is a strict descendent of b if a is a descendent of b but \(a \neq b\) The root node is an ancestor of all nodes
Example
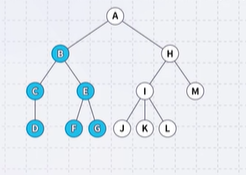
- The descendants of node B are B, C, D, E, F, and G
- The ancestors of node I are I, H, and A
Representation
List representation for child nodes (e.g.: linked list)
- Store the children with a list of pointers (or node indices).
source “K-MOOC 허재필 교수님의 <인공지능을 위한 알고리즘과 자료구조: 이론, 코딩, 그리고 컴퓨팅 사고> 강좌의 3-1 강좌의 트리 자료구조 중(http://www.kmooc.kr/courses/course-v1:SKKUk+SKKU_46+2020_T1)”
tags:
Comments
Post comment