Matrix Chain Multiplication

Matrix Chain Multiplication

Suppose A is \(k\times m\) and B is \(m\times n\)

• Then AB is \(k\times n\) and calculating AB is \(\Theta(kmn)\)
• The number of multiplications is given exactly \(kmn\) Suppose multiplication of three matrices ABC
• Matrix multiplication is associative so we may chose (AB)C or A(BC)
• The order of the multiplications may significantly affect the runtime If A and B are \(n \times n\) matrices and v is an n-dimensional column vector:
• Calculating (AB)v is \(\Theta(n^3)\)
• Calculating A(Bv) is \(\Theta(n^2)\)

Example: Multiply four matrices ABCD

• Many ways of parenthesizing this product
• Which has the least number of operations?

Consider these four:

Matrix	Dimensions
A	20\(\times\)5
B	5\(\times\) 40
C	40\(\times\) 50
D	50\(\times\)10

Considering each order: ex. ((AB)C)D

The required number of multiplication is:

• AB \(20\times5\times40=4000\)
• (AB)C \(20\times40\times50=40000\)
• ((AB)C)D \(20\times50\times10=10000\)

Total 54,000 multiplications

Repeating this for the last, we get the following table:

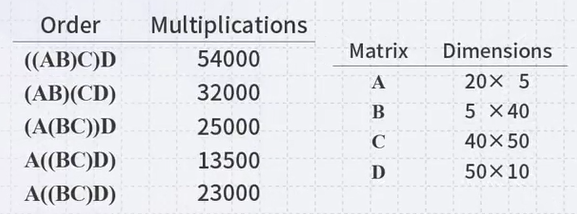
The optimal runtime uses A((BC)D)

In case of N multiplication: If we are multiplying \(A_{1}A_{2}A_{3}...A_{n}\), starting top-down, there are \(n-1\) different ways of parenthesizing this sequence:

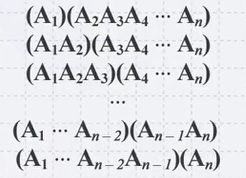
For each one:

• What is the work required to perform this multiplication
• What is the minimal amount of work required to perform both of the other products In finding the best product of \((A_{1}...A_{i})(A_{i+1}...A_{n})\) The work required is:
• The product columns(\(A_{1}\)) rows(\(A_{i}\) rows(\(A_{n}\))
  • Note that rows(\(A_{i}\)) and columns(\(A_{i+1}\)) must be equal Sub-problems:
• The minimal work required to multiply \(A_{i}...A_{i}\)
• The minimal work required to multiply \(A_{i+1}..A_{n}\) Similar to Fibonacci number, we can solve this with recursion

class MatricDim{
public:
  int nR, nC;
};

int Marix_Chain(MatrixDim *m, int s, int e){
  if(s==e){return 0;//when matrices are adjacent}
  else if(s+1==e){
    return m[s].nR * m[s].nC * m[e].nC;
  }
  else{}

  int minVal = INT_MAX;
  for(int i=s; i<e; i++){
    int currVal = Matrix_Chain(m, s, i);
    currVal += Matrix_Chain(m, i+1, e);
    currVal +=m[s].nR * m[i+1].nR * m[e].nC;
    minVal = std::min(minVal, currVal);
  }
  return minVal;
}

Because of the recursive nature, same problem with Fibonacci number: numerous occasions be asking for the optimal behavior of a given subsequence (overlapping subproblems) We can use memoization to solve this.

int Matrix_Chain_Memo(MatrixDim *m, int s, int e, int **memo){
  if(s==e){return 0;}
  else if(memo[s][e]==0){
    if(s+1==e){
      memo[s][e]=m[s].nR * m[s].nC * m[e].nC;
    }
    else{
      int minVal = INT_MAX;
      for(int i=sl i<e; i++){
        int currVal = Matrix_Chain(m, s, i);
        currVal += Matrix_Chain(m, i+1, e);
        currVal += m[s].nR * m[i+1].nR * m[e].nC;
      minVal = std::min(minVal, currVal);
      }
      memo[s][e] = minVal;
    }
  }
  else{}
  return memo[s][e];
}

Whenever we calculate s to e (i to j), if the value has been calculated once, return that value, only if not, we calculate the value. Runtime: \(O(n^3)\)

• We have \(n^2\) entries to compute and store

• For each entry, we need up to \(O(n)\) iterations. This is a top-down implementation.

• Bottom-up Implementation
  1. Matrix to store the best current solution from \(A_{i}\) to \(A_{j}\):

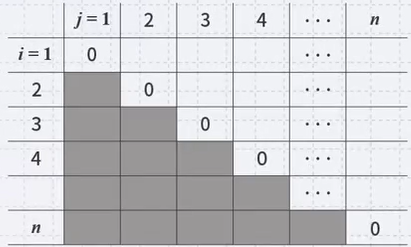
1. Calculating the minimum number of multiplications required for a specific sequence \(A_{i}...A_{j}\), we will fill the entry \(a_{ij}\) in the table

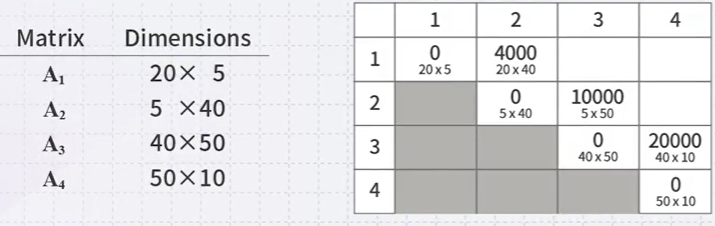
1. Calculate either: \(A_{1}(A_{2}A_{3})\) \((A_{1}A_{2})A_{3}\)

Continue to \(A_{2}(A_{3}A_{4})\) or \((A_{2}A_{3})A_{4}\)

Finally, \(A_{1}((A_{2}A_{3})A_{4})\) or \((A_{1}A_{2})(A_{3}A_{4})\) or \(A_{1}((A_{2}A_{3})A_{4})\)

Counting the number of calculations required (each \(\Theta(1)\)): \(n-1\) \((n-2)2\) \((n-3)3\)

Total time complexity: \(\sum_{i=1}^{n-1}(n-i)i=n\sum_{i=1}^{n-1}i-\sum_{i=1}^{n-1}i^{2}=\frac{n^3-n^2}{2}-\frac{n(n-1)(2n-1)}{6}=\frac{n^3-n}{6}\) Runtime: \(\Theta(n^3)\)

int Matrix_Chain_Iterative(MatrixDim *m, int n){
  int **d= new int * [n];
  for(int i=0; i<n; i++){
    d[i]=new int [n];
  }
  for(int i=0; i<n; i++)
    d[i][i]=0;
  for(int i=1; i<n; i++){
    for(int j=0; j<n-i; j++){
      d[j][j+i]=d[j][j]+d[j+i][j+i]+m[j].nR * m[j+1].nR * m[j+i].nC;
      for(int k=j+1; k<j+i; k++){
        int currVal=d[j][k]+d[k+1][j+i]+m[j].nR * m[k+1].nR * m[j+i].nC;
        d[j][j+i]=std::min(d[j][j+i].currVal);
      }
    }
  }
  int ret = d[0][n-1];
  for(int i=0; i<n; i++){delete [] d[i];} delete [] d;
  return ret;
}

source “K-MOOC 허재필 교수님의 <인공지능을 위한 알고리즘과 자료구조: 이론, 코딩, 그리고 컴퓨팅 사고> 강좌의 15-2 행렬 체인 곱셈 문제의 동적계획법 기반 해결 중(http://www.kmooc.kr/courses/course-v1:SKKUk+SKKU_46+2020_T1) “

back next

Comments

Post comment

Loading...