Critical Path

Critical Path

Suppose each task has a performance time associated with it

• If the tasks are performed serially, the time required to complete the task equals to the sum of the individual task times

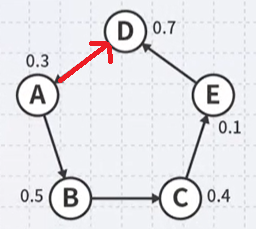
• These tasks require 0.3+0.7+0.5+0.4+0.1=2.0 s to execute serially

Suppose two tasks are ready to execute

• We could perform these tasks in parallel
• Computer tasks can be executed in parallel (multi-processing)
• Different tasks can be completed by different teams in a company

Suppose task A completes

• We can now execute tasks B and D in parallel
• However, task E cannot execute until task C completes, and task C cannot execute until task B completes
  • The least time in which these five tasks can be completed is 0.3+0.5+0.4+0.1=1.3s
  • This is called the critical time of all tasks
  • The path (A, B, C, E) is said to be the critical path

The program described shows the critical path in red

• We will define the critical time of each task to be the earliest time that it could be completed after the start of execution

Finding the Critical Path

• Tasks that have no prerequisites have a critical time equal to the time it takes to complete that task
• Tasks that depend on others, the critical time will be:
  • The maximum critical time that it takes to complete a prerequisite
  • Plus the time it takes to complete this task
• In this example, the critical times are:
  • task A completes in 0.3s
  • task B must wait for A and completes after 0.8s
  • task C must wait for A and completes after 1.0s
  • task C must wait for B and completes after 1.2s
  • task E must wait for both C and D, and completes after max(1.0, 1.2)+0.1=1.3s

Thus, we require more information:

• We must know the execution time of each task
• We will have to record the critical time for each task
  • Initialize these to zero
• We will need to know the previous task with the longest critical time to determine the critical path
  • Set these to null

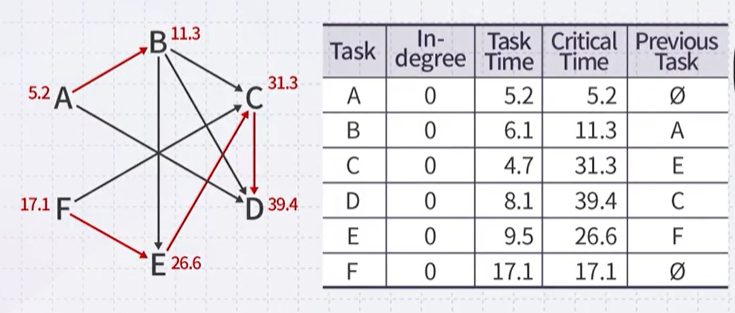
Suppose we have the following times for the tasks

Each time we pop a vertex v, in addition to what we already do:

• For v, add the task time onto the critical time for that vertex:
  • That is the critical time for v
• For each adjacent vertex w:
  • If the critical time for v is greater than the currently stored critical time for w
    • Update the critical time with the critical time for v
    • Set the previous pointer to the vertex v 1. Initialize the queue with those vertices with in-degree zero: A, F
      2. Pop task A and update its critical time 0.0+5.2=5.2
• For each neighbor of task A: B, D
  • Decrement the in-degree, push if necessary, and check if we must update the critical time:
    • B in-degree become zero, able to push to the queue.
    • Compare B and D with A’s critical time. Updates to greater one.
      1. Pop task F and update its critical time 0.0+17.1=17.1
• For each neighbor of task F:
  • Decrement the in-degree, push if necessary, and check if we must update the critical time 4. Pop task B and update its critical time 5.2+6.1=11.3
• For each neighbor of task B:
  • Decrement the in-degree, push if necessary, and check if we must update the critical time
  • Both C and E are waiting on F 5. Pop task E and update its critical time 17.1+9.5=26.6
• For each neighbor of task E:
  • Decrement the in-degree, push if necessary, and check if we must update the critical time 6. Pop task C and update its critical time 26.6+4.7=31.3
• For each neighbor of task C:
  • Decrement the in-degree, push if necessary, and check if we must update the critical time 7. Pop task D and update its critical time 31.3+8.1=39.4
• task D has no neighbors and the queue is empty
  • We are done

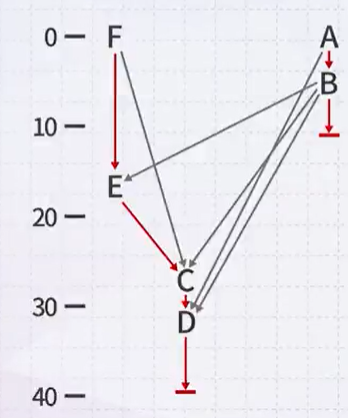
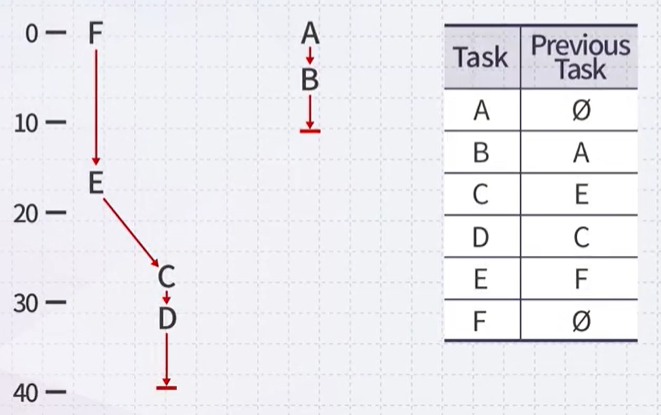
We can also plot the completing of the tasks in time

• We need to be able to execute two tasks in parallel for this example

Critical Path: F-E-C-D

• This path consumes the longest time (Longest Path)

Critical Time: Critical Time of D

• For faster process, improve some parts of FECD.
• The task and previous task defines a forest using the parental tree data structure

source “K-MOOC 허재필 교수님의 <인공지능을 위한 알고리즘과 자료구조: 이론, 코딩, 그리고 컴퓨팅 사고> 강좌의 14-2 임계 경로 중(http://www.kmooc.kr/courses/course-v1:SKKUk+SKKU_46+2020_T1)”

back next

Comments

Post comment

Loading...