Topological Sort

Motivation

Given a set of tasks with dependencies,

• Is there an order in which we can complete the tasks? Dependencies from a partial ordering
• A partial ordering on a finite number of objects can be represented as a directed acyclic graph (DAG)

Restriction of Paths in DAGs

In a DAG, given two different vertices \(v_{j}\) and \(v_{k}\), there cannot be both be a path from \(v_{j}\) to \(v_{k}\) and a path from \(v_{k}\) to \(v_{j}\)

Proof: Assume otherwise; thus there exists two paths \((v_{j}, v_{1.1}, v_{1.2}, v_{1.3}, ..., v_{k})\) \((v_{k}, v_{2.1}, v_{2.2}, v_{2.3}, ..., v_{j})\) From this, we can construct the path \((v_{j}, v_{1.1}, v_{1.2}, v_{1.3}, ..., v_{k}, v_{2.1}, v_{2.2}, v_{2.3}, ..., v_{j})\) This path is a cycle, but this is an acyclic graph \(\therefore\) contradiction

Definition of Topological Sorting

A topological sorting of the vertices in a DAG is an ordering \(v_{1}, v_{2}, v_{3}, ..., v_{\left|V\right|}\) such that \(v_{j}\) appears before \(v_{k}\) if there is a path from \(v_{j}\) to \(v_{k}\)

Given this DAG, a topological sort is

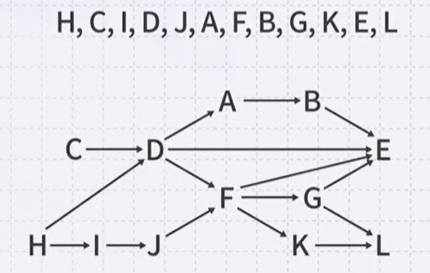
H, C have no in-degree, no dependencies

There are paths from H, C, I, D and J to F, so all these must come before F in a topological sort This sorting need not to be unique

Applications

Consider the course instructor getting ready for a dinner out wear: jacket, shirt, briefs, socks, tie, etc. constraints: pants after the briefs, socks before shoes

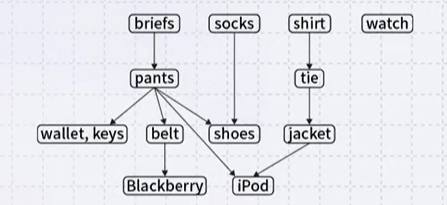
One topological sort: briefs, pants, wallets, keys, belt, socks, shoes, shirt, tie, jacket, iPod, watch A more reasonable topological sort: briefs, socks, pants, shirt, belt, tie, jacket, wallet, keys, iPod, watch, shoes

C++ header and source files have #include statements

• A change to an included file requires a recompilation of the current file
• On a large project, it is desirable to recompile only those source files that depended on those tiles which changed
• For large software projects, full compilations may take hours

Curriculum prerequisite

Topological Sort

Idea:

Given a DAG \(V\), make a copy \(W\) and iterate:

• Find a vertex v in W with in-degree zero
• Let v be the next vertex in the topological sort
• Continue iterating with the vertex-induced sub-graph \(W{v}\)

On this graph, iterate the following \(|V|\) = 12 times

• Choose a vertex v that has in-degree zero
• Let v be the next vertex in our topological sort
• Remove v and all edges connected to it

We can start from C or H Having completed task C, only H can be completed we can choose from D or I …

Thus, one possible topological sort would be: C, H, D, A< B, I, J, F, G, E, K or H, I, J, C, D, F, G, K, L, A, B, E

Analysis

Tools necessary for a topological sort

• Know and be able to update the in-degrees of each of the vertices
• table of the in-degrees of each of the vertices
• This requires : \(\Theta(\lvert V\rvert)\) memory

Iterate at least \(|V|\) times, so the runtime must be : \(\Omega(|V|)\)

• Find vertices with in-degree zero
• loop through the array with each iteration
• Runtime: \(O(\lvert V\rvert^{2})\)

Tree traversals

• Use a queue (or other container) to temporarily store those vertices with in-degree zero
• Each time the in-degree of a vertex is decremented to zero, push it onto the queue
• Scan through each of the vertices : \(\Theta(\lvert V\rvert)\)
• For each vertex, we will have to push onto and pop off the queue once, also \(\Theta(\lvert V\rvert)\)

Each value in the in-degree table is associated with an edge

• Here, \(\lvert E\rvert\)=16
• Each of the in-degrees must be decremented to zero
• The runtime of these operations is \(\Omega(\lvert E\rvert)\)
• If we are using an adjacency matrix: \(\Theta(\lvert V\rvert^{2})\)
• If we are using an adjacency list: \(\Theta(\lvert E\rvert)\)

Total runtime:

• If we use an adjacency list: \(\Theta(\lvert V\rvert+\lvert E\rvert)\)
• If we use an adjacency matrix: \(\Theta(\lvert V\rvert^{2})\)
• Memory requirement: \(\Theta(\lvert V\rvert)\)

Implementation

To implement a topological sort:

• Allocate memory for and initialize an array of in-degrees
• Create a queue and initialize it with all vertices that have in-degree zero

While the queue is not empty:

• pop a vertex from the queue
• decrement the in-degree of each neighbor
• those neighbors whose in-degree was decremented to zero are pushed onto the queue

Trick not to delete data from the queue and increasing the size of the queue in accordance with the number of the original vertices

• Initialization

Type array[vertex_size];
int ihead = 0, itail = -1;

• Testing if empty:

ihead == itail +1

• For push:

itail++;
array[itail] = next vertex;

• For pop: do not delete vertex

Type current_top = array[ihead];
ihead++;

Place each vertex into the queue exactly once

• Must never resize the array
• Do not have to worry about the queue cycling Because of the properties of a queue
• When finished, the underlying array stores the topological sort

Example

1. Initialize:
   • The array of in-degrees
   • The queue
2. Stepping through the table, push all source vertices into the queue
3. Pop the front of the queue
   • C has one neighbor: D
   • Decrement its in-degree
4. Pop H
   • H has two neighbors: D and I
   • Decrement their in-degrees
     • Both are decremented to zero, so push them onto the queue
5. Pop D
   • D has three neighbors: A, E and F
   • Decrement their in-degrees
     • A is decremented to zero, so push it onto the queue
6. Iterate this process
   • E, L have no neighbor: they are sink
7. When the queue is empty, we are done

The array stores the topological sorting

source “K-MOOC 허재필 교수님의 <인공지능을 위한 알고리즘과 자료구조: 이론, 코딩, 그리고 컴퓨팅 사고> 강좌의 14-1 DAG 구조와 활용 분야 중(http://www.kmooc.kr/courses/course-v1:SKKUk+SKKU_46+2020_T1)”

back next

Comments

Post comment

Loading...