Single-Source Shortest Path

Dijkstra Algorithm

Like Prim’s algorithm, we initially don’t know the distance to any vertex except the initial vertex

• We require an array of distances, all initialized to infinity except for the source vertex, which is initialized to 0
• Each time we visit a vertex, we will examine all adjacent vertices
  • We need to track visited vertices-a Boolean table of size \(\lvert V\rvert\)
• Do we need to track the shortest path to each vertex?
  • That is, do we have to store (A, B, F) as the shortest path to vertex F?
• We really only have to record that the shortest path to vertex F came from vertex B
  • We would then determine that the shortest path to vertex B came from vertex A
  • Thus, we need an array of previous vertices, all initialized to null

Iterate \(|V|\) times:

• Find that unvisited vertex v that has a minimum distance to it
• Mark it as having been visited
• Consider every adjacent vertex w that is unvisited:
  • Is the distance to v plus the weight of the edge (v, w) less than our currently known shortest distance to w
  • If so, update the shortest distance to w and record v as the previous pointer
• Continue iterating until all vertices are visited or all remaining vertices have a distance to them of infinity

Example

Find the shortest distance from (K) to every other vertices

Set up table:

• Which unvisited vertex has the minimum distance to it?

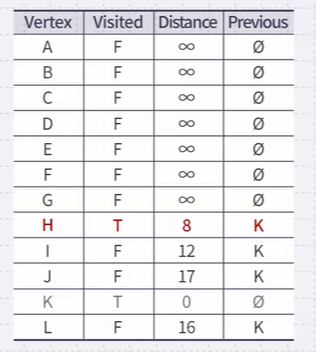
Vertex K has four neighbors: H, I, J and L Found at least one path to each of these vertices

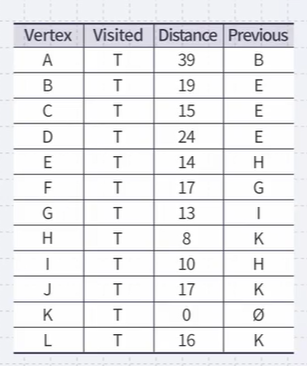
We have found the shortest path from vertex K to each of the other vertices. Using the previous pointers, we can reconstruct the paths

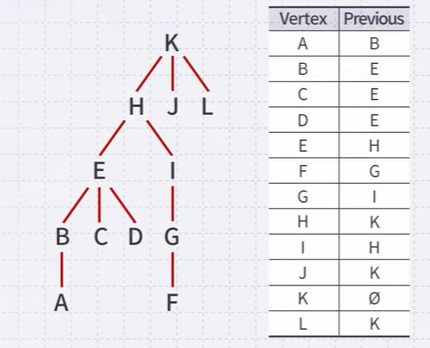
This table defines a rooted parental tree

• The source vertex K is at the root
• The previous pointer is the parent of the vertex in the tree

What if at some point, all unvisited vertices have a distance \(\infty\)?

• This means that the graph is unconnected
• We have found the shortest paths to all vertices in the connected subgraph containing the source vertex What if we just want to find the shortest path between vertices \(v_{j}\) and \(v_{k}\)?
• Apply the same algorithm, but stop when we are visiting vertex \(v_{k}\) Does the algorithm change if we have a directed graph?
• No

Implementation and Analysis

The initialization requires \(\Theta(\lvert V\rvert)\) memory and runtime Iterate \(\lvert V\rvert-1\) times, each time finding next closest vertex to the source

• Iterating through the table requires is \(\Theta(\lvert V\rvert)\) time
• Each time we find a vertex, we must check all of its neighbors
• With an adjacency matrix, the runtime is \(\Theta(\lvert V\rvert(\lvert V\rvert+\lvert V\rvert))=\Theta(\lvert V\rvert^{2})\)
• With an adjacency list, the runtime is \(\Theta(\lvert V\rvert^{2}+\lvert E\rvert)=\Theta(\lvert V\rvert^{2})\) as \(\lvert E\rvert=O(\lvert V\rvert^{2})\)

To do better: We only need the closest vertex

How about a priority queue?

• Assume we are using a binary heap
• We will have to update the heap structure - this requires additional work

The initialization still requires \(\Theta(\lvert V\rvert)\) memory and runtime - The priority queue will also requires \(O(\lvert V\rvert)\) memory - We must use an adjacency list, not an adjacency matrix

We iterate \(\lvert V\rvert\) times, each time finding the closest vertex to the source - Place the distances into a priority queue - The size of the priority queue is \(O(\lvert V\rvert)\) - Thus, the work required for this \(O(\lvert V\rvert \lg \lvert V\rvert)\)

Is this all the work that is necessary? - Each edge visited may result in a new edge being pushed to the very top of the heap - Thus, the work required for this is \(O(\lvert E\rvert \lg \lvert V\rvert)\) Total runtime: \(O(\lvert V\rvert \lg(\lvert V\rvert)+\lvert E\rvert \lg(\lvert V\rvert))=O(\lvert E\rvert \lg(\lvert V\rvert))\)

source “K-MOOC 허재필 교수님의 <인공지능을 위한 알고리즘과 자료구조: 이론, 코딩, 그리고 컴퓨팅 사고> 강좌의 13-2 다익스트라 알고리즘과 복잡도 중(http://www.kmooc.kr/courses/course-v1:SKKUk+SKKU_46+2020_T1)”

back next

Comments

Post comment

Loading...