Shortest Path
by mervyn
Motivation
Suwon to Busan: throws back the shortest path when input the starting and the end point.
Dijkstra’s Algorithm
Dijkstra’s algorithm solves the single-source shortest path problem
- It is very similar to Prim’s algorithm
- Assumption: all the edge weights are positive
Strategy
Suppose that you are at vertex A
- You are aware of all vertices adjacent to it
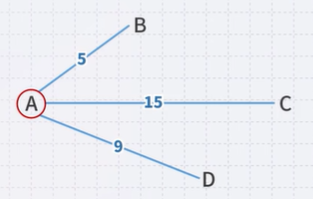
- Is 5 the shortest distance to B via the edge (A, B)?
- Are you guaranteed that the shortest path to C is (A, C), or that (A, D) is the shortest path to vertex D?
Accept (A, B) is the shortest path to B from A
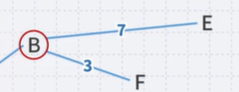
- (A, B, F) is the shortest path from A to F?
- Are we guaranteed that any other path we are currently aware of is going to be the shortest path?
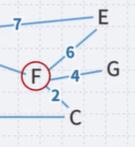
- (A, B, F, E) is longer than (A, B, E)
- (A, B, F, C) is shorter than the path (A, C)
At this point, we have the shortest distances to B and F
- In undirected, weighted graph, if the weight of all edges increased by 1, the shortest path would change.
source “K-MOOC 허재필 교수님의 <인공지능을 위한 알고리즘과 자료구조: 이론, 코딩, 그리고 컴퓨팅 사고> 강좌의 13-1 그래프 최단경로 알고리즘 중(http://www.kmooc.kr/courses/course-v1:SKKUk+SKKU_46+2020_T1)”
tags:
Comments
Post comment