Disjoint Sets

Disjoint-Set Data Structure

A disjoint-set data structure maintains a collection \(C={S_{1}, S_{2}, ..., S_{k}}\) of disjoint dynamic sets. Each set is identified by a representative which is some member of the set.

Operations

• make-set(x) creates a new set whose only member is x
• union-set(x, y) takes the union of sets that contains x and y
• find-set(x) returns the representative of the set containing x If find-set(x)==find-set(y), then the objects x and y are in the same disjoint set

Connected Components

Given a graph:

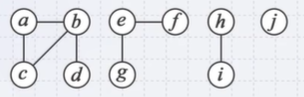
For each edge (x, y), perform union-set (x, y)

Note that, connected components can be computed more efficiently by using DFS

Implementation

Alternative implementation: Let each disjoint set be represented by a tree

• The root of the tree is the representative object

• To take the union of two such sets, simply attach one tree to the root of the other
• If the height of one tree is larger, add the other tree under that
• If the heights are equal, it doesn’t matter which tree goes under. In this case, the height of the result will always be +1 of the height of the trees
• If union_set(u, v) u, v are already in the same tree, no movement needed.

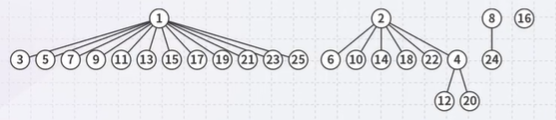
• find-set and union-set are now both \(O(h)\) Normally, a node points to its children. However, as we are only interested in the root; therefore, our interest is in storing the parent. Assume we are creating disjoint sets the n integers 0, 1, 2, …, n-1

Define an array

parent -= new int [n];
for(int i=0; i<n; i++){
  parent[i]=i;
}

If parent[i]==i, then i is a root node

• Initially, each integer is in its own set
• Find-set function

int Find_Set(int x){
  while(parent[x] !=x){
    x=parent[x];
  }
}
return x;

Complexity: \(T_{find}(n)=O(h)\)

• Union-set function

void Union_Set(int x, int y){
  x=Find_Set(x);
  y=Find_Set(y);

  if(x != y){
    parent[y]=x;
  }
}

Complexity: \(T_{union}(n)=2T_{find}(n)+\Theta(1)=O(h)\)

Optimization

To optimize both find-set and union-set, we must minimize the height of the tree

• Therefore, point the root of the shorter tree to the root of the taller tree
• The height of the taller will increase if and only if the trees are equal in height

Worst-Case scenario

The worst-case disjoint set. Attaching the tree with less height to the root of the tree with greater height, the worst case must occur when both trees are equal in height - where all the trees to be combined are always the same.

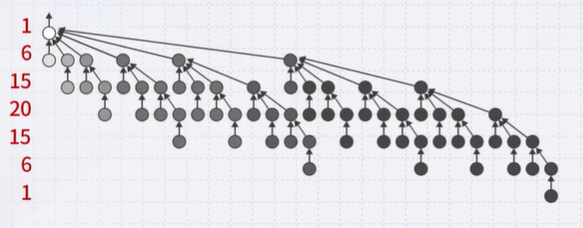
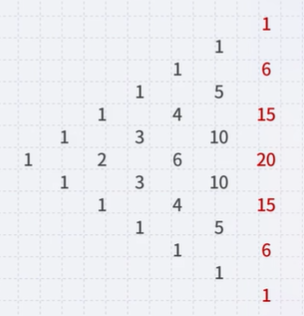
These are binomial trees, defining Pascal’s triangle

• The binomial coefficients

\[\binom{n}{m}= \begin{cases} 1, & m=0 \text{ or } m=n\\ \binom{n-1}{m}+\binom{n-1}{m-1}, & 0<m<n \end{cases}=\frac{n!}{m!(n-m)!}\]

Suppose we have a worst-case tree of height h

• We need the number of nodes and the average depth of a node \(\sum_{k=0}^{h}\binom{h}{k}=2^{k}=n\) \(\sum_{k=0}^{h}k\binom{h}{k}=h2^{h-1}\)
• Therefore, the average depth is \(\frac{h2^{h-1}}{2^{h}}=\frac{h}{2}=\frac{lg(n)}{2}\)
• The height and average depth of the worst case are \(O(lg(n))\)

Best-Case scenario

All elements point to the same entry with a resulting height of \(\Theta(1)\):

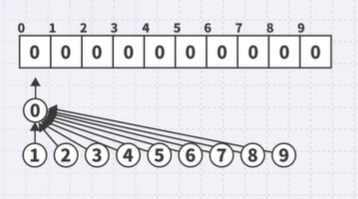
source “K-MOOC 허재필 교수님의 <인공지능을 위한 알고리즘과 자료구조: 이론, 코딩, 그리고 컴퓨팅 사고> 강좌의 12-1 서로소 집합 중(http://www.kmooc.kr/courses/course-v1:SKKUk+SKKU_46+2020_T1)”

back next

Comments

Post comment

Loading...