Minimum Spanning Trees: Prim's Algorithm

Motivation

Road construction to connect all cities: How to minimize construction cost? Road construction plan to collect all the cities with the minimum cost.

Spanning Trees

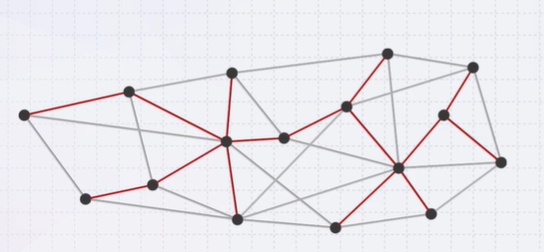
This spanning tree is not unique. Such a collection of edges is called a tree because if any vertex is taken to be the root, we form a tree by treating the adjacent vertices as children, and so on…

Spanning trees on Weighted Graphs

The weight of a spanning tree is the sum of the weights on all the edges which comprise the spanning tree

Minimum Spanning Tree(MST)

Spanning tree which minimizes the weight

Unweighted Graphs

Observation

• In an unweighted graph, we nominally give each edge a weight of 1
• Consequently, all minimum spanning trees have weight \(\lvert V\rvert-1\)

Algorithms

Two common algorithms for finding minimum spanning trees are:

• Prim’s algorithm
• Kruskal’s algorithm Greedy algorithms make decisions only based on each moment. In MST problem, Prim’s algorithm and Kruskal’s algorithm retrieve the optimal solution.

Prim’s Algorithm

• Strategy: Given a single vertex \(v_{1}\), it forms a minimum spanning tree on one vertex. Add that adjacent vertex \(v_{2}\), that has a connecting edge \(e_{1}\) of minimum weight
  • This forms a minimum spanning tree on our two vertices and \(e_{1}\) must be in any minimum spanning tree containing the vertices \(v_{1}\) and \(v_{2}\)

Suppose we have a known minimum spanning tree on \(k<n\) vertices

• How to extend this minimum spanning tree?

Add that edge \(e_{k}\) with least weight that connects this minimum spanning tree to a new vertex \(v_{k+1}\)

• This creates a minimum spanning tree on \(k+1\) nodes - there is no other edge we could add that would connect this vertex
• Does the new edge, however, belong to the MST on all n vertices?

Suppose it does not

• Thus, vertex \(v_{k+1}\) is connected to the MST via another sequence of edges

Because a MST is connected, there must be a path from vertex \(v_{k+1}\) back to our existing MST

• It must be connected along some edge \(\widetilde{e}\)

Let w be the weight of this MST

• When we chose to add \(v_{k+1}\), it was because \(e_{k}\) was the edge connecting an adjacent vertex with least weight
• Therefore \(\lvert\widetilde{e}\rvert > \lvert e_{k}\rvert\) where \(\lvert e\rvert\) represents the weight of the edge e

Suppose we swap edges and instead choose to include \(e_{k}\), and exclude \(\widetilde{e}\)

• The result is still a MST, but the weight is now \(w+ \lvert e_{k}\rvert - \lvert\widetilde{e}\rvert\leq w\) Thus, by swapping \(e_{k}\) for \(\widetilde{e}\), we have a spanning tree that has less weight than the so-called MST containing \(\widetilde{e}\)
• This contradicts our assumption that the spanning tree containing \(\widetilde{e}\) was minimal
• Therefore, our minimum spanning tree must contain \(e_{k}\)
  1. Start with an arbitrary vertex to form a MST on one vertex
  2. At each step, add a vertex v not yet in the MST that has an edge with least weight that connects v to the existing minimum spanning sub-tree
  3. Continue until we have n-1 edges and n vertices
• Implementation
  • Initialization:
    1. Select a root node and set its distance as 0
    2. Set the distance to all other vertices as \(\infty\)
    3. Set all vertices to being unvisited
    4. Set the parent pointer of all vertices to 0
  • Iterate while there exists an unvisited vertex with distance \(<\infty\)
    1. Select an unvisited vertex with minimum distance
    2. Mark that vertex as having been visited
    3. For each adjacent vertex, if the weight of the connecting edge is less than the current distance to that vertex
       • Update the distance to equal the weight of the edge
       • Set the current vertex as the parent of the adjacent vertex
  • Halting Conditions
    • There are no unvisited vertices which have a distance \(< \infty\)
    • If all vertices have been visited, we have a spanning tree of the entire graph
    • If there are vertices with distance \(\infty\), then the graph is not connected and we only have a MST of the connected sub-graph containing the root

Example

Find the MST for the following undirected weighted graph

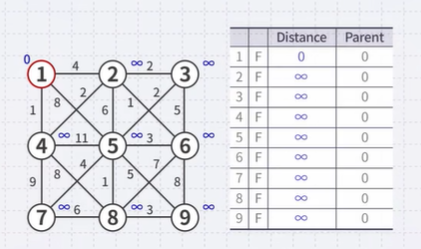
1. Set up the appropriate table and initialize it
2. We could extend the trivial tree containing just the root node by one of the three possible children:

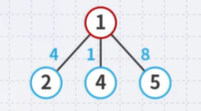
As we wish to find a minimum spanning tree, it makes sense we add that vertex with a connecting edge with least weight.

1. The next unvisited vertex with minimum distance is vertex 4
   • Update vertices 2, 7, 8
   • Don’t update vertex 5

We have updated all vertices adjacent to vertex 4.

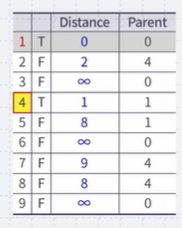
1. We could extend the tree by adding one of the edges (1,5), (4,2), (4,7), or (4,8)
   • When there are no more unvisited vertices, we are done
   • If at any point, all remaining vertices had a distance of \(\infty\), this would indicate that the graph is not connected
     • In this case, the MST would only span one connected sub-graph
2. Using the parent pointers, we can now construct the minimum spanning tree

Summary

• Begin with a vertex which represents the root
• Starting with this trivial tree and iteration, we find the shortest edge which we can add this already existing tree to expand it This is a reasonably efficient algorithm: the number of visit to vertices is kept to a minimum

Analysis

The initialization requires \(\Theta(|V|)\) memory and runtime. We iterate \(\lvert V\rvert-1\) times, each time finding the closet vertex

• Iterating through the table requires is \(\Theta(\lvert V\rvert)\) time
• Each time we find a vertex, we must check all of its neighbors
• With an adjacency matrix, the runtime is \(\Theta(\lvert V\rvert(\lvert V\lvert +\lvert V\rvert))=\Theta(\lvert V\rvert^{2})\)
• With an adjacency list, the runtime is \(\Theta(\lvert V\rvert^{2}+\lvert E\rvert)=\Theta(\lvert V\rvert^{2})\) as \(\lvert E\rvert=O(\lvert V\rvert^{2})\)

To do better:

• We only need the shortest edge next
• Priority queue?
  • Assume we are using a binary heap
  • We will have to update the heap structure=this requires additional work

Analysis with Priority Queue (Minimum Heap)

The initialization requires \(\Theta(|V|)\) memory and runtime

• The priority queue will also requires \(O(\lvert V\rvert)\) memory

We iterate \(\lvert V\rvert-1\) times, each time finding the closest vertex

• Place the shortest distances into a priority queue
• The size of the priority queue is \(O(\lvert V\rvert)\)
• Thus, the work required for this is \(O(\lvert V\rvert\lg(\lvert V\rvert))\)

The each edge visited may result in a new edge being pushed to the very top of the heap. Thus, the work required for this is \(O(\lvert E\rvert\lg(\lvert V\rvert))\)

Total runtime: \(O(\lvert V\rvert\lg(\lvert V\rvert)+ \lvert E\rvert\lg(\lvert V\rvert))=O(\lvert E\rvert\lg(\lvert V\rvert))\)

If number of edges are critically larger than vertices, using priority queue could cost more than without it. However, if there are just a moderate number of edges (not extremely more than vertices) priority queue could be a more efficient way.

source “K-MOOC 허재필 교수님의 <인공지능을 위한 알고리즘과 자료구조: 이론, 코딩, 그리고 컴퓨팅 사고> 강좌의 11-1 최소신장트리 문제와 프림 알고리즘 중(http://www.kmooc.kr/courses/course-v1:SKKUk+SKKU_46+2020_T1)”

back next

Comments

Post comment

Loading...