Quick Sort

Strategy

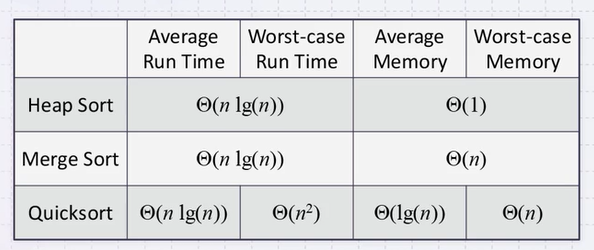
We have seen two \(\Theta(n lg(n))\) sorting algorithms:

• Heap sort which allows in-place sorting, and
• Merge sort which is faster but requires more memory

We will now look at a recursive algorithm which may be done almost in place but which is faster than heap sort

• Use an object in the array (a pivot) to divide the two
• Average case: \(\Theta(n lg(n))\) time and \(\Theta(lg(n))\) memory
• Worst case: \(\Theta(n^2)\) time and \(\Theta(n)\) memory

We will look at strategies for avoiding the worst case

Quicksort

Merge sort

• Splits the array sub-lists and sorts them
• The larger problem is split into two sub-problems based on location in the array (quicksort divide based on its size to values smaller than that and values bigger than that)

Consider the following alternative:

• Chose an object in the array and partition the remaining objects into two groups relative to the chosen entry

Runtime Analysis

Like merge sort, we can either:

• Apply insertion sort if the size of the sub-list is sufficiently small, or
• Sort the sub-lists using quicksort In the best case, the list will be split into two approximately equal sub-lists, and thus, the runtime could be very similar to that of merge sort: \(\Theta(n lg(n))\)
• Worst-case scenario
  • If we choose the smallest element as our pivot, we still have to sort a list of size n-1: \(T(n)=T(n-1)+\Theta(n)=\Theta(n^2)\) Thus, the runtime drops from n lg(n) to n^2 To avoid worst case, choose the median element in the list as the pivot. Unfortunately, it’s difficult to find.
• Alternative strategy: take the median of a subset of entries
  • For example, take the median of the first, middle, and last entries (median-of-three)

Median-of-Three

1. Sorting the elements based on the middle entry results in two sub-lists, each of which must be sorted (again, using quicksort).
2. Undergoes partitioning based on median-of-three, and find the median-of-three from those median-of-threes
3. Starting from the front, the values smaller than the median-of-three filled in from the left. The values larger than the median-of-three filled in from the right.
4. Once finished, copy the median-of-three into the resulting hole.

In-place Implementation

1. Examine the first, middle, and last entries and choose the median of these to be the pivot. In addition, we can:
   • move the smallest entry to the first entry
   • move the largest entry to the middle entry
2. Partition all remaining elements based on whether they are smaller than or greater than the pivot Find two entries:
   • One larger than the pivot (starting from the front)
   • One smaller than the pivot (starting from the back) which are out of order and then swap them
3. Continue doing so until the appropriate entries you find are actually in order
   • The index to the larger entry we found would be the first large entry in the list (as seen from the left)
   • Therefore, we could move this entry into the last entry of the list
   • We can fill this spot with the pivot

template <typename Type>
void Quicksort(Type *_array, int _first, int _last){
  if(_last - _first <= NUM_THRESHOLD){
    Insertion_Sort<Type>(&_array[_first], _last-_first);
  }
  else{
    Type pivot = Find_Pivot<Type>(_array, _first, _last);
    int low= _first +1;
    int high= _last -2;
    while(_array[low]<pivot){low++;}
    while(_array[high]>pivot){high--;}
    while(low<high){
      std::swap(_array[low], _array[high]);
      low++; high--;
      while(_array[low]<pivot){low++;}
      while(_array[high]>pivot){high--;}
    }
    _array[_last-1] = _array[low];
    _array[low]=pivot;
    Quicksort(_array, _first, low);
    Quicksort(_array, high, _last);
  }
}

Memory Requirements

• The additional memory requirement is \(\Theta(lg(n))\)
  • Each recursive function call places its local variables, parameters, etc., on a stack
    • The depth of the recursion tree is \(\Theta(lg(n))\)
• Unfortunately, if the runtime is \(\Theta(n^2)\)< the memory use is \(\Theta(n)\)

source “K-MOOC 허재필 교수님의 <인공지능을 위한 알고리즘과 자료구조: 이론, 코딩, 그리고 컴퓨팅 사고> 강좌의 10-2 힙 정렬 중(http://www.kmooc.kr/courses/course-v1:SKKUk+SKKU_46+2020_T1)”

back next

Comments

Post comment

Loading...