Heap Sort
by mervyn
Heap Sort
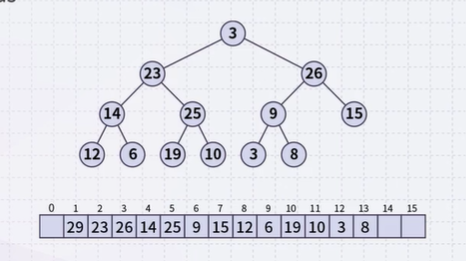
- Inserting n objects into a min-heap and then taking n objects will result in them coming out in order
- Strategy: given an unsorted list with n objects, place them into a min-heap, and take them out
Analysis of Heap Sort
- Taking an object out of a heap with n times requires \(O(lg(n))\) time.
- Therefore, taking n objects out requires \(\sum_{k=1}^{n}lg(k)=lg\left ( \prod_{k=1}^{n} k \right )=lg(n!)\)
- Heap sort requires only a constant amount of space.
- Heap sort does not require as much external memory
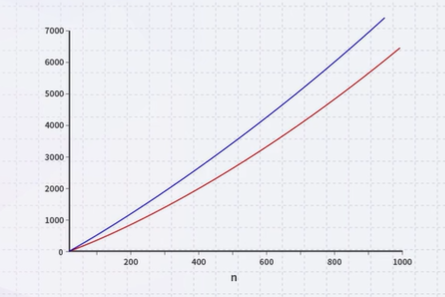
\(lg(n!)\) and \(nlg(n)\)
A plot of \(lg(n!)\) and \(nlg(n)\) suggests that they are asymptotically related:
In-place Implementation
- Problem: This solution requires additional memory, that is, a min-heap of size n
- This requires \(\Theta(n)\) memory and is therefore not in place
- Is it possible to perform a heap sort in place, that is, require at most \(\Theta(1)\) memory (a few extra variables)?
- Instead of implementing a min-heap, consider a max-heap:
- A heap where the maximum element is at the top of the heap and the next to be popped
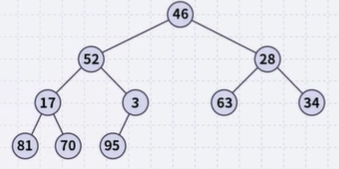
- Consider this unsorted array: [46 52 28 17 3 63 34 81 70 95]
- This array represents the following complete tree:
- This is neither a min-heap, max-heap, or binary search tree
Additionally, because arrays start at 0 (we started at entry 1 for binary heaps), we need different formulas for the children and parent.
- The formulas are now:
- Children: 2k+1 and 2k+2
- Parent: (k-1)/2
Can we convert this complete tree into a max-heap?
- Restriction: The operation must be done in-place
Let’s work bottom-up: each leaf node is a max heap on its own
- Starting at the back, we note that all leaf nodes are trivial heaps.
- Also, the subtree with maximum number of the root is a max-heap
- Percolating down and/or swap
- Starting with the next higher level, percolating down and/or swap
- The final product is a max-heap
Analysis of Heapify
Considering a perfect tree of height h:
- The maximum number of swaps which a second-lowest level would experience is 1, the next higher level, 2, and so on
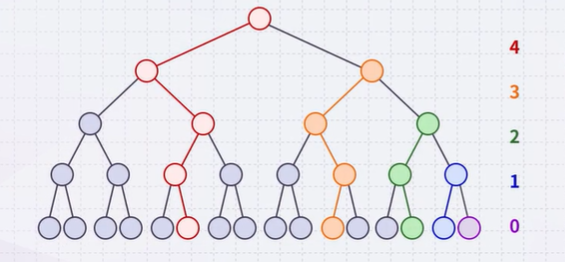
At depth k, there are \(2^k\) nodes and in the worst case, all of these nodes would have to percolated down h-k levels
- In the worst case, this would requiring a total of \(2k(h-k)\) swaps
Writing this sum mathematically, we get: \(\sum_{k=0}^{h}2^{k}(h-k)=(2^{h+1}-1)-(h+1)\)
Recall that for a perfect tree, \(n=2^h+1-1\) and \(h+1=lg(n+1)\), therefore \(\sum_{k=0}^{h}2^{k}(h-k)=n-lg(n+1)\)
Each swap requires two comparisons (which child is greatest), so there is a maximum of \(2n\) (or \(\Theta(n)\)) comparisons
Example: Heap Sort
Convert unordered array with n=10 elements into a max-heap [46 52 28 17 3 63 34 81 70 95] None of the leaf nodes need to be percolated down, and the first non-leaf node is position \(n/2\)
- Compare 3 with its child and swap them
- Compare 17 with its two children and swap it with the maximum child (70) …
- Converted the unsorted array into a max-heap [95 81 63 70 52 28 34 17 46 3]
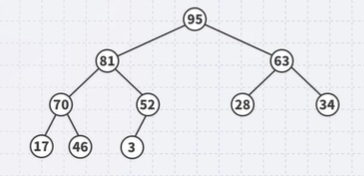
- Pop the maximum element of this heap: gap at the back of the array
- Fill the last entry in the array with the largest element
- Repeat this process: pop the maximum element, and then insert it at the end of the array (pop and append)
Summary
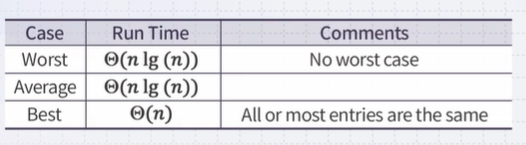
- Heapification runs in \(\Theta(n)\) (linear time)
- Popping n items from a heap of size n, runs in \(\Theta(n lg(n))\) time
- We are only making one additional copy into the blank left at the end of the array
- Therefore, the total algorithm will run in \(\Theta(n lg(n))\) time
- No worst-case scenarios
- Dequeuing from the heap will always require the same number of operations regardless of the distribution of values in the heap
- One best case: if all the entries are identical, then the runtime is \(\Theta(n)\)
- The original order may speed up the heapification, however, this would only speed up an \(\Theta(n)\) portion of the algorithm
source “K-MOOC 허재필 교수님의 <인공지능을 위한 알고리즘과 자료구조: 이론, 코딩, 그리고 컴퓨팅 사고> 강좌의 10-1 힙 정렬 중(http://www.kmooc.kr/courses/course-v1:SKKUk+SKKU_46+2020_T1)”
tags:
Comments
Post comment