Problem1_2

Problem

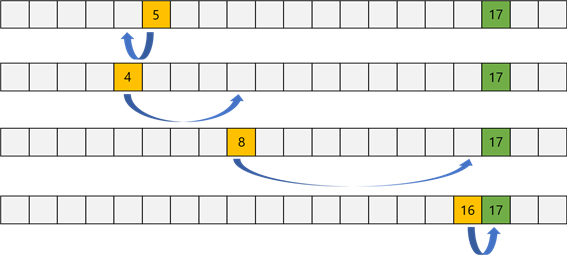
• On number line, when the current point is X, the next movement is one of X+1, X-1, 2*x. It takes 1 second for each movement.

• Given the current point X and target point D, print out minimum seconds required for reaching to the target point. (0 <= X, D <= 100,000)

  • Example Input: 5 17
  • Example Output: 4

source “ K-MOOC 허재필 교수님의 <인공지능을 위한 알고리즘과 자료구조: 이론, 코딩, 그리고 컴퓨팅 사고> 강좌의 과제1 중(http://www.kmooc.kr/courses/course-v1:SKKUk+SKKU_46+2020_T1)”

Algorithm

Shortest time from X to D

1. count shortest path –> BFS
   • shortest path = shortest path of parent +1
2. create queue, enqueue starting position (let’s call it node)
   • if X == D, print 0
3. else, loop till the queue is empty
   • pop next unvisited node from queue
   • If the popped node is destination node, return it
   • else, mark current node as visited, and for each of 3 possible movements, enqueue each valid movement into the queue with +1 distance

---

header: , ,... array: row=[-1, +1, *2], swap//+x number line: 0 <= x, d <= 100,000 how to count steps???// starting point (0) + first shortest path (1) + shortest path from first shortest path (1) +....

Coding

#include <iostream>
#include <queue>
#include <array>
#include <set>// int X, D are elements of array[100001]

using namespace std;
int arr[100001];

bool Arr(int x)
    {
        set<int> s{ begin(arr), end(arr) };
        for (int i = 0; i < 100001; i++)
        {
            arr[i] = i;//[0, 1, 2 ... , 100000];
        }
        return true;
   }


struct Node
{
    Node(int x, int dist = 0) : x(x), distance(dist) {}

    //'distance' represents its minimum distance from the source.
    int x;
    int distance;

    //If you want to conveniently put objects in a  set or a map,
    //they must provide a less-than operator.
    bool operator<(const Node& o) const {
        return x < o.x || x == o.x;
    }
};

int BFS(Node X, Node D)
{   
    set<Node> visited;

    queue<Node> q;
    q.push(X);

    while (!q.empty())
    {
        Node node = q.front();
        q.pop();

        int X = node.x;
        int dist = node.distance;
        int row[] = { 1, -1, X };

        if (X == D.x )
            return dist;

        else if (!visited.count(node))
        {
            visited.insert(node);
            {
                //check for all 3 possible movements and enqueue each valid movement into the queue.
                for (int i = 0; i < 3; i++)
                {
                    int x1 = X + row[i];

                    if (x1 >= 0 && x1 < 100001)
                        q.push({ x1, dist + 1 });
                }
            }

        }
    }
}

int main()
{
    Node X = { 5 };

    Node D = { 17 };

    cout << "Minimum number of steps required is " << BFS(X, D);
    cout << endl;
    return 0;
}

References “https://www.techiedelight.com/chess-knight-problem-find-shortest-path-source-destination/#:~:text=Given%20a%20chess%20board%2C%20find,given%20destination%20from%20given%20source.&text=The%20idea%20is%20to%20use,Below%20is%20the%20complete%20algorithm.”

Comments

Post comment

Loading...